同変ニューラルネットワークの解説：その２- 群の誘導表現による深層学, SteerableCNN

はじめに

前回では、群上で行う畳み込みによる Group Convolution の定義をしました．それが、正則表現という線形群作用に対して同変になることを確認しました．それには、以下の２つの問題がありました

入力のデータタイプや中間層での表現がスカラー場に限られる．
1. 特徴マップ $\small f:\mathbb{R}^2 \rightarrow \mathbb{R}^C$ は枚数 $\small C$ のスカラー場として扱われている．
群が大きくなると、それに伴って計算量が増えてしまう．
1. 群の正則表現に限られるているので、パラメータが膨張しやすい．
2. 連続的である無限群には対応できない．

1への対策としてSteerableCNN では、まず中間層の特徴マップがより一般的なベクトル場として表現されるようにベクトル場を普段機械学習で扱われるユークリッド空間とは異なる多様体上に組み込めるようにファイバー束（より正確には (主束に)同伴したベクトル束の切断 (Section of Associated Vector Bundle) ）を用いて表します．SteerableCNNで扱うデータの多様体は、比較的規則性が高く対称性を効率的に活用できるものに限られています．例として２次元画像( $\small \mathbb{R}^2$ ) や球面( $\small S^2$ )が挙げられます．ニューラルネットワークのフィードフォワード演算子をベクトル場を同変的に変換するものに限定することでスカラーの場に限らず、ベクトル場の特徴マップも正しく扱うことを可能にしています．

2への対策は、群 $\small G$ 全てを使うのではなく、より小さい部分群 $\small H$ のみを使って、 $\small H$ から $\small G$ の誘導表現を作成するので、群 $\small G$ が大きくなっても計算量の膨張が緩和されます．そして、Group Convolutionでは Lifting Layer を用いて $\small G$ の空間上で中間層で処理を行うため、群の大きさに応じて中間層の次元が膨張する傾向にありますが、SteerableCNNでは等質空間 $\small G/H$ 上で中間層の処理を行っており、これはLiftingを必要とせず、入力データと同じドメインで処理を行うことになります．群が連続である場合は、無限数のフィルターが想定されますが、それを有限数にある基底たちの線型結合で表すこと(steerable フィルター)で連続的な演算子の近似を可能にしています．

今回の説明は、主に[1]と[2]の論文の内容をかなり嚙み砕いて、幾つかの要点のみを記載したものです．大まかな全体像をつかむ事を目的にしていますので、より詳しく学びたい方は論文をご覧ください．数学の詳細は、[3]と[4]がお勧めです．

等質空間≅剰余空間

音響は一次元上 ( $\small \mathbb{R}$ ) の配列データであり、画像は一般的に2次元ユークリッド空間上 ( $\small \mathbb{R}^2$ ) のデータであります．その他にも、地球上の天候データやパノラマ画像は球面上（ $\small S^2$ ）のデータです．これらの構造は高い規則性を持っています．2次元画像上で任意の2点、AとBを考えた時、並進変換の作用( $\small (\mathbb{R}^2, +)$ 群の作用 )を用いれば容易にAからBへ移動できます．同じく、球面上の任意の2点、AとBの間も回転の作用 ( $\small SO(3)$ 群の作用 ) で移動できます．このように、集合 $\small X$ の任意の点と点へ群 $\small G$ の作用によって移動できる作用を推移的 ( transitive )であると言い、 $\small X$ は $\small G$ の等質空間と呼ばれます．

上記のように、等質空間 $\small X$ と固定部分群による剰余類 $\small G/H_x$ との間に同型写像が存在することで、これらが同型であることが示されています．これが意味するのは「群の作用」という枠組み上、これらは全く相違ない数学的オブジェクトとして扱うことができます．

深層学習での実例を考えると、画像の $\small \mathbb{R^2}$ 面は等質空間であり、 $\small G$ から回転群を剰余した剰余空間として扱うことができます．

ベクトル場による特徴マップ

ここから、深層学習に用いられる中間層表現を等質空間上のベクトル場をファイバー束を用いて表します．これには、厳密な定義が必要となりますが長くなるので、ここでは割愛させていたたき、詳しくは[3]を参考にして下さい．

中間層のベクトル場は「主束に同伴したベクトル束」によって定義されます．ザックリとした説明になりますが、この主束は、剰余空間 $\small G/H_x$ を底空間 ( base space )として持っており、その上に基底と、それらがどのように変換するかの情報を持っています．しかし、ベクトルの成分の情報は備わっていません．そこに、ベクトルの成分を加味して、それらが基底の変換に対して正しく変換されるように同値関係で制約を設けたのが主束に同伴したベクトル束です．

以下のように、以前のGroup Convolutionではベクトル成分が回転変換に対して正しく変換せず、正しくベクトルを扱うことが出来ませんでした．同伴したベクトル束という構造を組み込むことで (その同値関係により )、ベクトル場が(1)から(3)へ正しく変換されます．

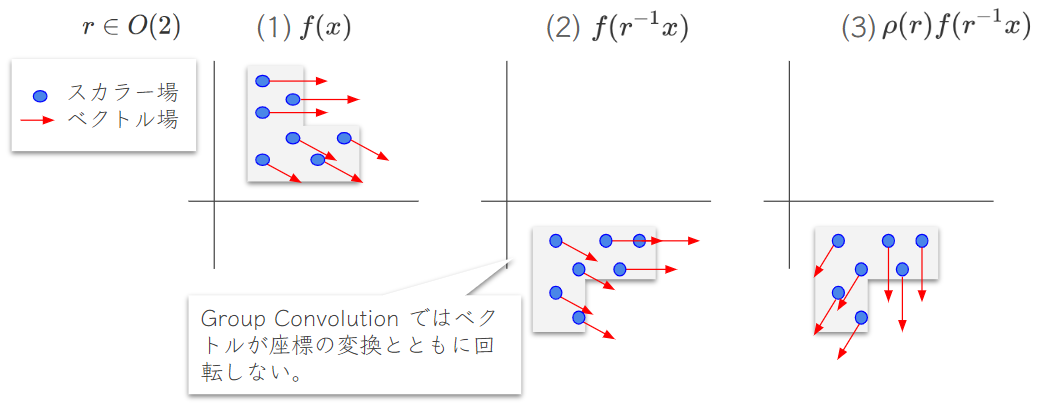
誘導表現

主束に同伴したベクトル束上のペア、 $\small (g,v)$ に現れるベクトルの成分 $\small v$ を各点 $\small g \in G$ で定義すると関数 $\small f:G \rightarrow V$ で表せます．ベクトルの成分には、同値関係による制約があるので、それを満たした関数の集合 $\small \mathcal{I}_{G}$ を扱うことに絞れば、常に制約を満たすことができます．この集合はマッキー関数の集合と呼ばれます．

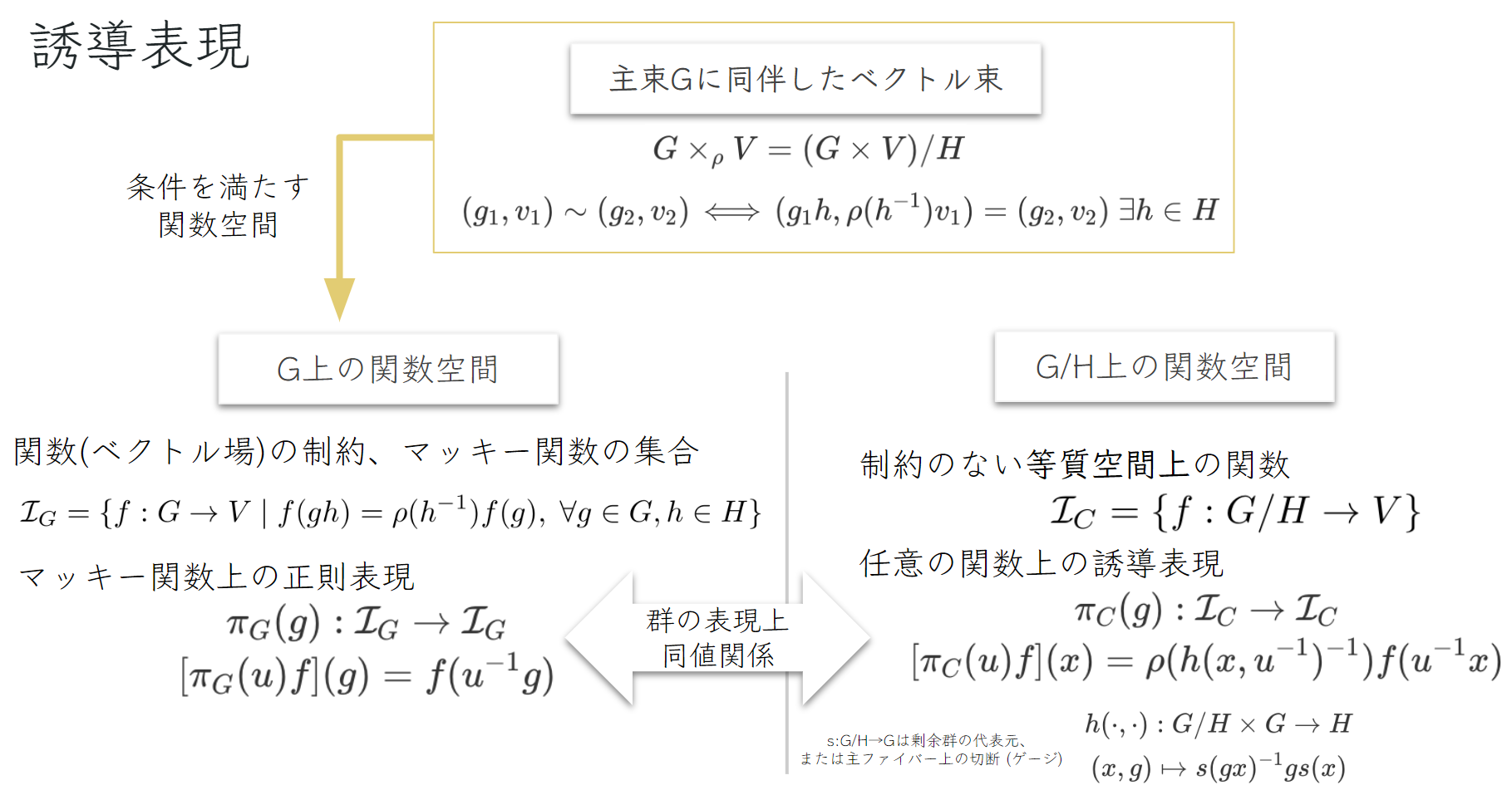
ここで面白いのは、マッキー関数上の正則表現は、「制約のない等質空間上の関数」上の誘導表現と等価することです．以下のように、表現 $\small (\pi_G,\mathcal{I}_G)$ と $\small (\pi_C,\mathcal{I}_C)$ の間には同型写像が存在するので、「群の表現」という枠組み上、これらは同一のものとして扱うことができます．SteerableCNNでのフィードフォワード処理は $\small (\pi_C,\mathcal{I}_C)$ の誘導表現と可換することが同変性を満たすための条件となります．

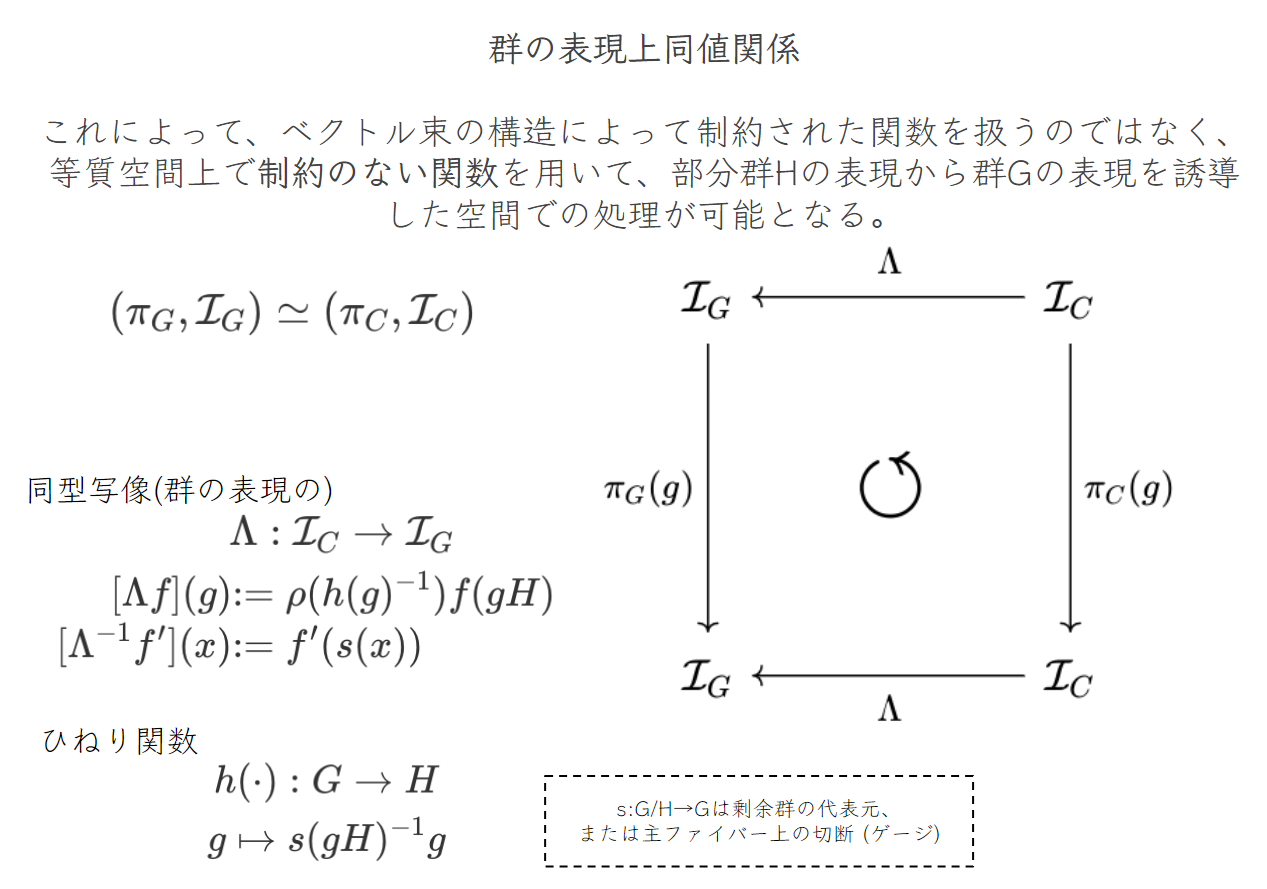
これによって見えてくることは、

Group Convolutionでは、lifting layerなどを用いて群G上での処理へ持ち上げる必要があったが、SteerableCNNでは等質空間、または剰余空間で処理を行うので元のデータと同じドメインで処理を行えるようになる．
群 $\small G$ を使うのではなく、より小さな固定部分群 $\small H$ から群 $\small G$ の表現を構築している．

SteerableCNN

一般的なSteerableCNNの定義と画像上で扱われる例は以下となります．

これから簡単な例として等質空間が画像である場合をより詳しく見ていきましょう．具体的なニューラルネットワークのフィードフォワード処理の演算子を明記して、同変性を満たすための条件を定義していきます．

フィードフォワード処理が畳み込み（※正確には相互相関だが畳み込みという名で根付いてしまっている．）
である場合、以下のように、それが誘導表現と可換することが同変性の条件となります．

ここで、畳み込み処理が使われる数学的な理由があります．フィードフォワード処理が線形である場合、同変性を満たす全ての処理は畳み込み処理で表すことが可能である「All you need is convolution」という定理が存在します．よって、他の演算を考慮せずとも一般性を失わず、畳み込み処理に絞ることができます．

カーネルの線形制約が満たされればカーネルは同変となります．この制約により：

各点 $\small x$ にて、カーネルのパラメータは、 $\small \mathbb{R}^C_{out} \times \mathbb{R}^C_{in}$ の部分空間となる．カーネルの自由度が下がり、学習パラメータが削減される．
よって、基底 $\small \{\psi_i(x)\}$ さえ分かれば学習の重み $\small {w_i}$ との線形結合、 $\small k(x)=\sum_i w_i \psi_i(x)$ がカーネルとなる．

ここからは、General E(2) Equivariant CNN[2] で紹介されている具体的なフィードフォワード処理を見ていきましょう．主な流れは、上記の群の表現による、カーネルの線形制約を細かく既約表現に分解して、各既約表現に対して事前に算出された基底を使ってカーネルを構築します．

まずは、カーネルの制約を行列で以下のように細かく表します．従来のCNNはチャンネル数がハイパーパラメータとなりますが、SteerableCNNでは、使う部分群 $\small H$ と群の表現の集合 $\small \{ \rho_i \}$ となります．

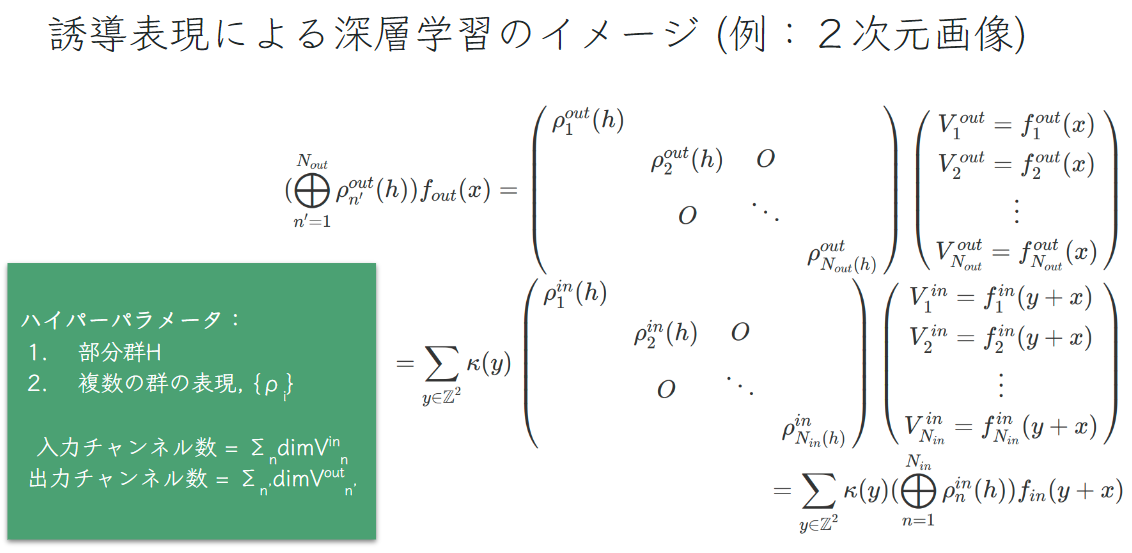
扱う部分群 $\small H$ は固定部分群であり、一般的にコンパクトな位相群 ( $\small SO(2)$ など)
を使います．コンパクトな位相群はPeter-Weylの定理によって既約表現へと分解が可能です．イメージとしてこの分解は、シグナル処理ではお馴染みのフーリエ分解と同様で、それよりも一般的な分解と捉えることができます．フーリエ分解は、群が実数の加法群のモジュロ1であり、既約表現が $\small \{e^{2 \pi kx} \}_{k\in \mathbb{Z}},\ x\in G$ で $\small G$ 上の自乗可積分函数を分解する既約分解の特殊ケースとなります．

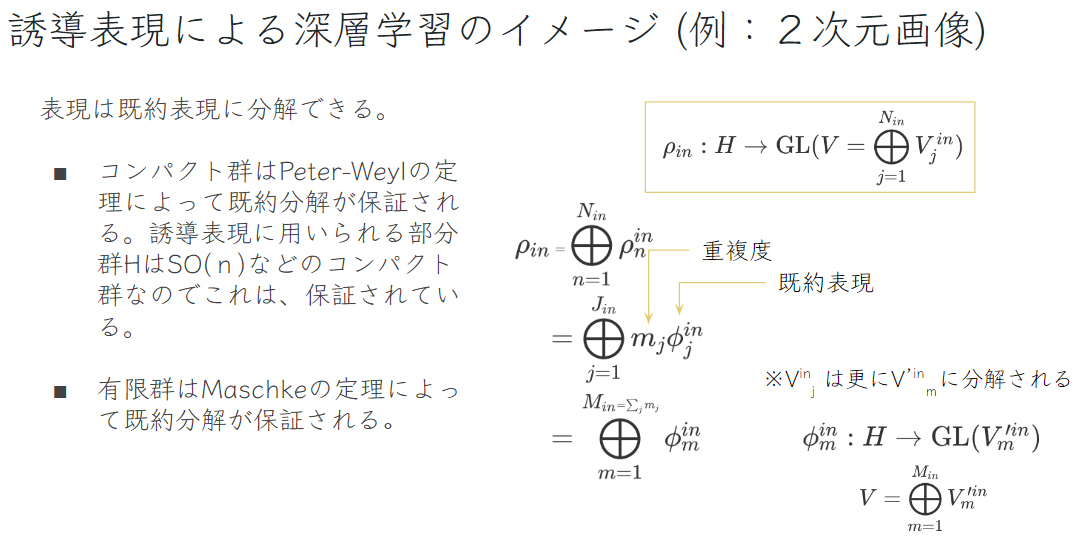
以前のカーネルの制約を既約表現で置き換えると以下のようになります．

分解することによって、カーネルの制約を各入力・出力既約表現のセットで独立に扱うことができます．最後に以下のように、各入力・出力既約表現のセットに対して既に計算されている基底を表から選択して、重みとの線形結合したものが同変性を満たしたカーネルとなります．

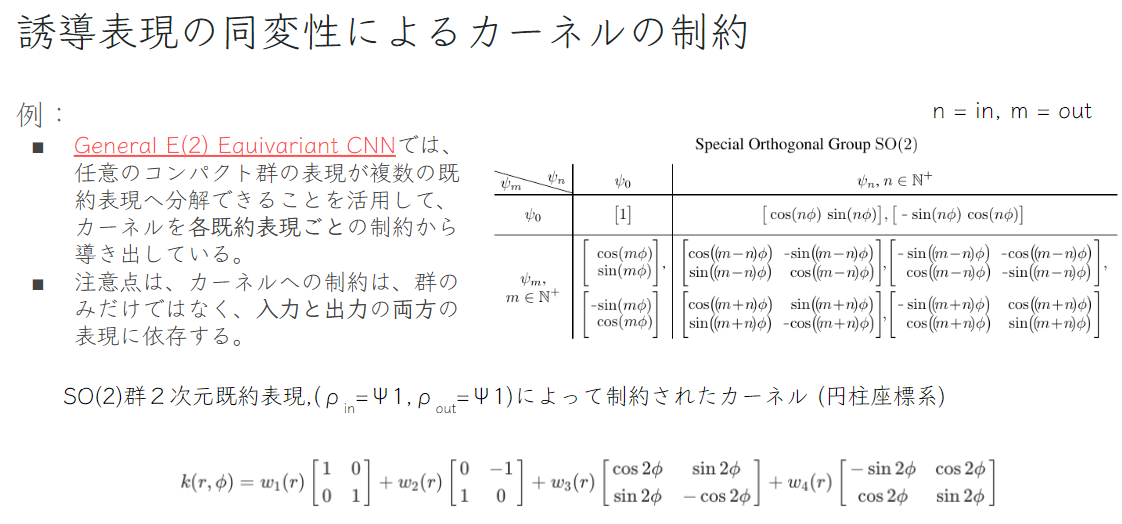
※ 限度は、深層学習など演算は基本実数なので複素表現が用いられていない．

SteerableCNNの活性化関数

活性化関数も同変性を満たさなくてはなりません．中間表現のベクトル場の方向を保ったまま、ノルムの大きさだけを変化させる処理に絞れば簡単に同変性を満たした活性化関数を作成することができます．

群の選択と帰納バイアス

同変ニューラルネットワーク全般に群が大きければ大きい程、帰納バイアスが強くなる傾向にあります．

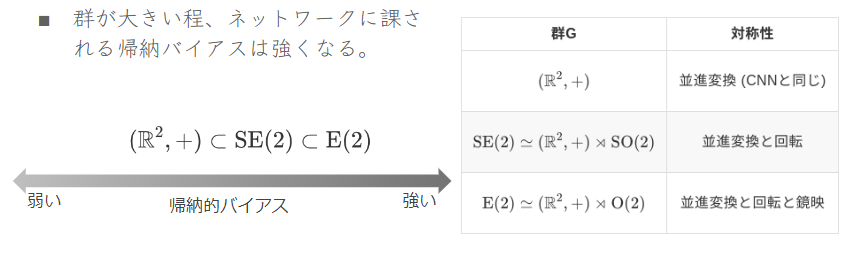
強い方がより多くの対称性が活用され学習パラメータが削減され、それらの対称性に纏わる汎化性も高まります．一方、データに対して誤った帰納バイアスが課された場合は精度の悪化が起きます．

例えば、MNISTの例では鏡映の同変性を組み込んだ場合、0,1,8以外の数字は反転したら意味が異なる数字なので、鏡映は相応しくない対称性となります．しかし、スケールが小さい下層では文字全体の形を見ているのではなく、局所的なテキスチャーを見ているの鏡映を組み込んでも問題ないと思われます．より大きなスケールを見る上層には、帰納バイアスを緩和させて鏡映の同変性を破るようにすることが可能です．

まとめ

Steerable CNNでは、中間層の特徴マップをベクトル場（主束に同伴したベクトル束）で表現される．
等質空間は群の作用によって移動できる空間であり、剰余空間と同型である．
以前のGroup Convolutionでは、ベクトル成分が回転変換に対して正しく変換されず、ベクトルを扱うことができなかったが、SteerableCNNでは同伴したベクトル束を組み込むことで正しい変換が可能になる．
SteerableCNNでは、等質空間または剰余空間で処理を行うため、元のデータと同じドメインで処理が行える．
SteerableCNNでは、群Gではなくより小さな固定部分群Hから群Gの表現を構築している．
フィードフォワード処理が線形である場合、同変性を満たす全ての処理は畳み込み処理で表すことが可能である．
カーネルの線形制約が満たされれば、カーネルは同変であり、学習パラメータが削減される．
[2]のSteerableCNNの例では、群の表現によるカーネルの線形制約を既約表現に分解し、基底を使ってカーネルを構築する．
活性化関数も同変性を満たさなくてはならない．ベクトルの方向に作用せずにノルムのみに作用させれば良い．
群が大きい方が帰納バイアスが強くより多くの対称性が活用され学習パラメータが削減されるが、誤った帰納バイアスが課されると精度が悪化する．
MNISTの例では、鏡映の同変性は文字の形が現れるスケール上では相応しくないが、スケールが小さい下層では適用できるので、それに応じて途中の層で対称性を破るような設計が可能である．

参考文献:

[1] T. S. Cohen, M. Geiger, and M. Weiler, “Intertwiners between Induced Representations (with Applications to the Theory of Equivariant Neural Networks),” arXiv:1803.10743 [cs, stat], Mar. 2018, Accessed: Jun. 27, 2021. [Online]. Available: http://arxiv.org/abs/1803.10743

[2] M. Weiler and G. Cesa, “General $\small E(2)$ -Equivariant Steerable CNNs,” arXiv:1911.08251 [cs, eess], Apr. 2021, Accessed: Apr. 16, 2021. [Online]. Available: http://arxiv.org/abs/1911.08251

[3] 小林俊行, 大島利雄, リー群と表現論. 岩波書店, 2005.

[4] J.-P. Serre, Linear representations of finite groups, Corr. 5th print. New York: Springer-Verlag, 1996.