ここでは、トピックに絞って複数の関連性がある論文を同次に紹介しています.流れが少しでも把握できるように、一番新しいものから並べています.論文の概要やQ&A形式を用いて要点を記載しており、OpenReviewが既存であれば、意見をまとめたものを投稿しています.気になる論文の選択に役立ったら良いと思います.論文を読む前に幾つかの要点を把握することで、皆さんが内容を素早く吸収できることを目的としています.
生物の形態形成を模擬した、ニューラル・オートマトンによる自己組織化に感動しました.以下のリンクで、育ったり自己再生していくオートマトンが楽しめます.

ここで紹介する、ニューラル・オートマトンに関連する最近の論文は以下の4本となります.
- Growing Steerable Neural Cellular Automata (発行日:2023年02月19日)
- E(n)-equivariant Graph Neural Cellular Automata (発行日:2023年01月25日)
- Growing Isotropic Neural Cellular Automata (発行日:2022年05月03日)
- Goal-Guided Neural Cellular Automata: Learning to Control Self-Organising Systems (発行日:2022年04月25日)
Growing Steerable Neural Cellular Automata
著者:Ettore Randazzo, Alexander Mordvintsev, Craig Fouts
発行日:2023年02月19日
最終更新日:2023年02月19日
URL:http://arxiv.org/pdf/2302.10197v1
カテゴリ:Neural and Evolutionary Computing, Artificial Intelligence, Machine Learning
概要:
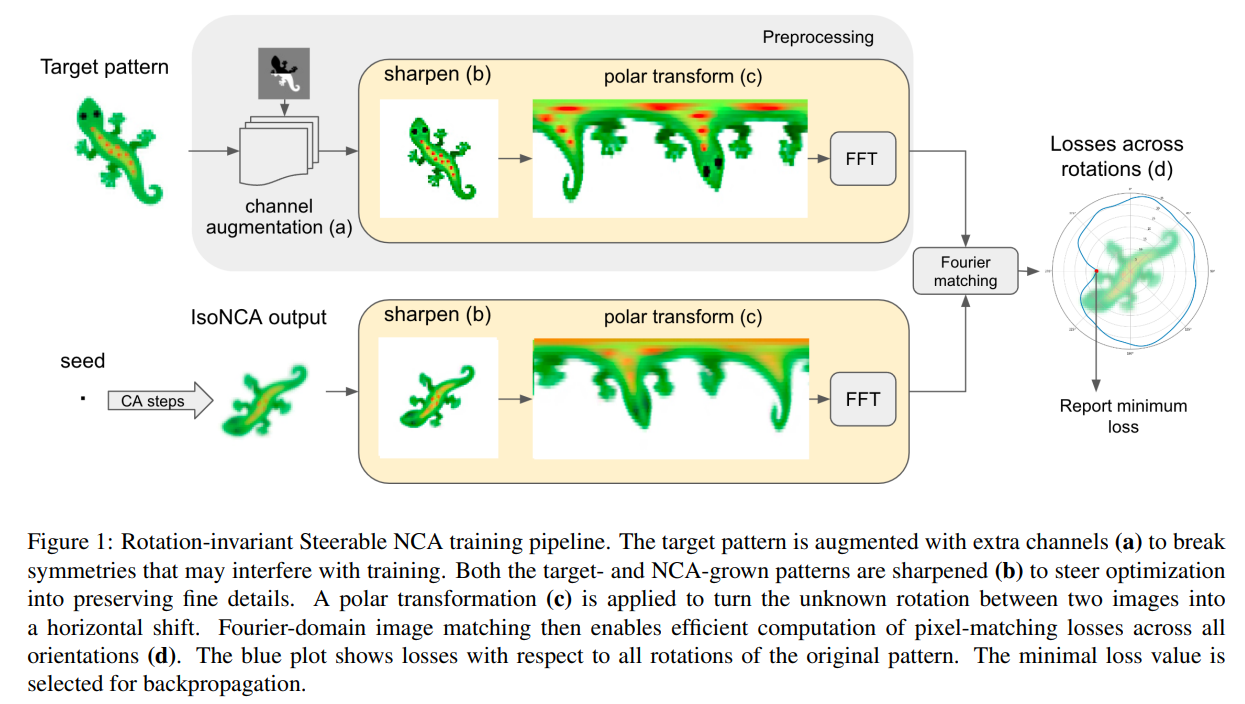
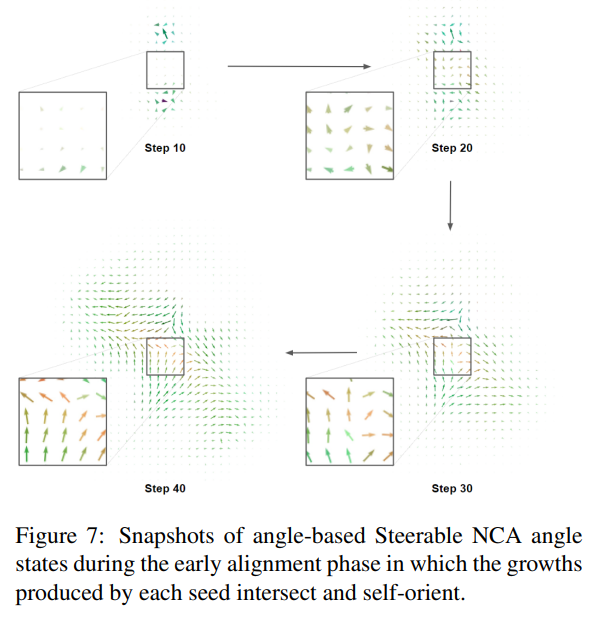
ニューラル・セルラーオートマトン(NCA)モデルは、局所的な調整から生じる複雑なグローバルな振る舞いやパターン形成の能力が注目されています.ただし、NCAのオリジナルの実装では、細胞は自分自身の方向調整ができず、外部からの指定が必要でした.最近は、等方性NCA(Growing Isotropic Neural Cellular Automata)と呼ばれるバリアントも開発されました.これにより、モデルの向きに依存しなくなりました.しかし、本研究では、異なるアプローチを用いてNCAを見直し、調整可能な内部状態によって「回転」できるようにして、各細胞を自己の向きに責任を持たせました.結果として、Steerable NCAは、同じパターンに埋め込まれた異なる向きの細胞を含むことができます.そのため、等方性NCAは方向に関して無関心であるのに対し、Steerable NCAはキラリティを持ち、左右の対称性が事前に決定されています.本研究では、(1) 2つのシードだけを使用して対称性を崩す、または(2)非同期の細胞更新を利用して上下対称性を崩すために回転不変のトレーニング目標を導入する方法など、より具体的な手法についても述べられています.
Q&A:
Q: Growing Steerable Neural Cellular Automata」という論文の目的は何でしょうか?
A: 本論文の目的は、ニューラル・セルラー・オートマトン(NCA)を再考し、各セルが自身の方向性に責任を持つようにし、調整可能な内部状態によって決定される「回転」を可能にすることで、ステアラブルNCAモデルを実現することである.本論文では、この新しいモデルの特徴と挙動を探求し、オリジナルのNCAや等方性NCAと比較します.また、本論文で紹介した実験を簡単に再現するためのGoogle Colabsのセットも提供しています.
Q: Mordvintsevら(2022)の研究が明示した、完全等方性パターン成長のトレーニングの問題点は何ですか?
A: Mordvintsevら(2022)の研究では、あらゆるターゲットパターンに固有の回転・反射対称性など、完全等方性パターン成長のトレーニングに関する問題を明示的に扱っています.(1)構造化シードによって初期条件となるシステムの上下左右の対称性を崩すこと、(2)新規の回転・反射不変の損失を導入し、他のいくつかの機能拡張と並行してトレーニングを容易にする、という2つの代替アプローチでこれらの問題を解決しました.
Q: IsoNCAについて、他のグリッドベースNCAとの違いについて詳しく教えてください.
A: IsoNCAは、従来のグリッドベースのNCAであり、細胞は不動で、その知覚は任意に遠ざけることのできない局所近傍によって制限される.他のグリッドベースのNCAと異なる点は、他のNCAが異方性、つまり細胞が何らかの外的要因に方向依存するのに対し、等方性になるように構築できる点です.
Q: ニューラル・セルラー・オートマトンはどのようなタスクで成功しているのか、またその例を教えてください.
A: ニューラルセルラーオートマトン(NCA)は、数字の分類、テクスチャーの生成、形態形成、敵対的攻撃、制御システムなど、様々なタスクで成功を収めている.例えば、MNISTの数字の自己分類、テクスチャの自己組織化、3Dアーティファクトや機能的な機械の成長、カートポールエージェントをロバストに制御するためのNCAの使用などである.
Q: Steerable NCAモデルは、どのようにトレーニング体制を簡略化し、スピードアップするのでしょうか?
A: ステアラブルNCAモデルは、IsoNCAが2つの対称性の破れを必要とするのに対し、1つの対称性の破れしか必要としないため、トレーニング体制を簡素化し高速化し、より速いターゲット形状成長とトレーニング時間をもたらします(例えば、安定し整ったトカゲは、同じトレーニング構成で等方性バリエーションが30000ステップなのに対し、ステアラブルバリアントがわずか10000トレーニングステップ).
Q: Steerable NCAモデルにおいて、グリッドセルはどのように表現されているのでしょうか?
A: A:ステアブルNCAモデルのグリッドセルは、Cがチャネル数であり、最初の4つのチャネルが可視性のあるRGBAイメージを表すベクトルによって表されます.各セルの状態は、ベクトルs=[s0=R;s1=G;s2=B;s3=A;:::;sC-1]によって表されます.
Q: Steerable NCAモデルにおいて、Grid Cellの状態はどのように更新されるのでしょうか?
A: A:ステアラブルNCAモデルのグリッドセルの状態は、3×3ムーア近傍の情報のみを用いて繰り返し更新され、セルの更新はNCAステップごとに確率的に起こり、確率はpupdとなります.
Q: αチャネルとは何か、また、細胞が現在「生きている」のか「空っぽ」なのかを判断する上でどのような役割を果たすのか.
A: Steerable NCAモデルのアルファチャンネルは、セルが現在「生きている」か「空」かを決定します.アルファ値(A)が0.1より大きいか、3×3近傍に少なくとも1つの生きているセルがある場合、セルは生きているとみなされる.空っぽのセルの状態は、各NCAステップの後に明示的にゼロに設定される.
Q: 細胞の周りの状態に関する情報はどのように収集され、どのようなフィルターが使用されますか?
A: 各セルは、チャンネルごとの離散3×3ラプラシアンフィルターKlapと、x軸とy軸のそれぞれに対するソーベルフィルターKxとKyの3つのフィルターを用いて、その近隣の状態についての情報を収集する.ラプラシアンフィルターは、セルの状態とその近傍の平均状態との差を計算し、ソーベルフィルターはそれぞれの軸に沿った状態の勾配に関する情報を蓄積する.
Q: ラプラシアンフィルターとは何か、また、あるセルの状態とその近傍の平均的な状態との差をどのように計算するのか.
A: ラプラシアンフィルターは、Steerable NCAモデルにおいて、あるセルの状態とその近傍の平均状態との差を計算するために使用されます.これは、トレーニングの速度とパフォーマンスを向上させるために、知覚の段階で追加されます.ラプラシアンフィルターは、セル自身の状態から近隣の平均状態の2倍を差し引くことで、状態の2次導関数を計算する.この差に定数係数Klapを乗じるが、このモデルでは2に設定されている.
Q: Growing NCAにおいて、状態勾配はどのように回転されるのか、またその目的は何か.
A: グローイングNCAでは、状態の勾配を所定の角度だけ回転させ、それに対応して回転したX軸、Y軸の勾配を認識する.この回転の目的は、近傍の空間状態の勾配を認識することである.
Q: 本作品で取り上げたSteerable NCAの2つのバリエーションは、どのように異なる方法で同じ目的を達成しているのでしょうか?
A: 本作品で取り上げたステアラブルNCAの2つのバリエーションは、回転不変の損失と並行して2つの異なるシードまたは単一のシードを配置することで初期化されます.両者は異なる方法で上下対称性を破り、その結果、よりシンプルで高速な学習レジームを実現する.
Q: 知覚がソーベルフィルタのみで構成されているモデルにラプラシアンフィルタを追加することで、学習速度や性能はどのように向上するのか?
A: ラプラシアンフィルタを追加することで、ソーベルフィルタのみで認識されるモデルに対して、学習スピードとパフォーマンスが大幅に向上します.ラプラシアンフィルターが具体的にどのような効果をもたらすかは、文脈上明記されていない.
Q: 本稿で紹介した方法は、従来の方法と比較してどのようなメリットがあるのでしょうか?
A: 「Growing Steerable Neural Cellular Automata」で紹介した方法は、各セルが自身の向きを調整することで、同じパターンの中に様々な向きが埋め込まれたSteerable NCAを実現しています.この方法は、従来の等方的なNCAに比べて、向きにとらわれないため、よりシンプルで高速な学習が可能であるという利点があります.さらに、Steerable NCAはキラリティを持つため、対称性を破ったトレーニングや回転不変のトレーニング目標を導入することが可能です.
Q: 本論文の実用的な貢献は何ですか?
A: 論文「Growing Steerable Neural Cellular Automata」では、NCA(Neural Cellular Automata)の新しいアプローチとして、セルが自らの向きを調整できる「Steerable NCA」を紹介しています.このアプローチの実用的な貢献は、従来のNCAモデルでは不可能であった、同じパターンの中に様々な向きのセルを埋め込んだパターンを生成できることである.また、論文で紹介した実験を再現するためのGoogle Colabsのセットも提供しています.
Q: 本論文の理論的な貢献は何ですか?
A: 「Growing Steerable Neural Cellular Automata」論文の理論的な貢献は、各セルが自身の向きに責任を持ち、調整可能な内部状態によって決定される「旋回」を可能にすることで、様々な向きのセルを含むSteerable NCAモデルを実現することです.本論文では、ステアラブルNCAモデルの機能を紹介する実験も行っています.
Q: 実験やデータ解析で得られた主な知見は何ですか?
A: 細胞が自ら向きを調整できる「Steerable Neural Cellular Automata (NCA)」という新しいモデルの開発について解説しています.これは、細胞が自分の向きを調整することができず、モデル設計者が外部から向きを調整しなければならない、オリジナルのNCAモデルとは対照的なものです.本記事では、グリッドセル、確率的更新、調整可能な内部状態など、ステアラブルNCAモデルの主要な特徴について解説しています.また、論文で紹介された実験を再現するために、Google Colabsのセットが利用可能であることにも触れています.
Q: 本稿で紹介した新手法の実装はどこにあるのでしょうか?
A: 「Growing Steerable Neural Cellular Automata」で紹介した新しい手法の実装は、Github(https://github.com/google-research/self-organising-systems/tree/master/isotropic_nca)で見ることができます.
E(n)-equivariant Graph Neural Cellular Automata
著者:Gennaro Gala, Daniele Grattarola, Erik Quaeghebeur
発行日:2023年01月25日
最終更新日:2023年01月25日
URL:http://arxiv.org/pdf/2301.10497v1
カテゴリ:Machine Learning
概要:
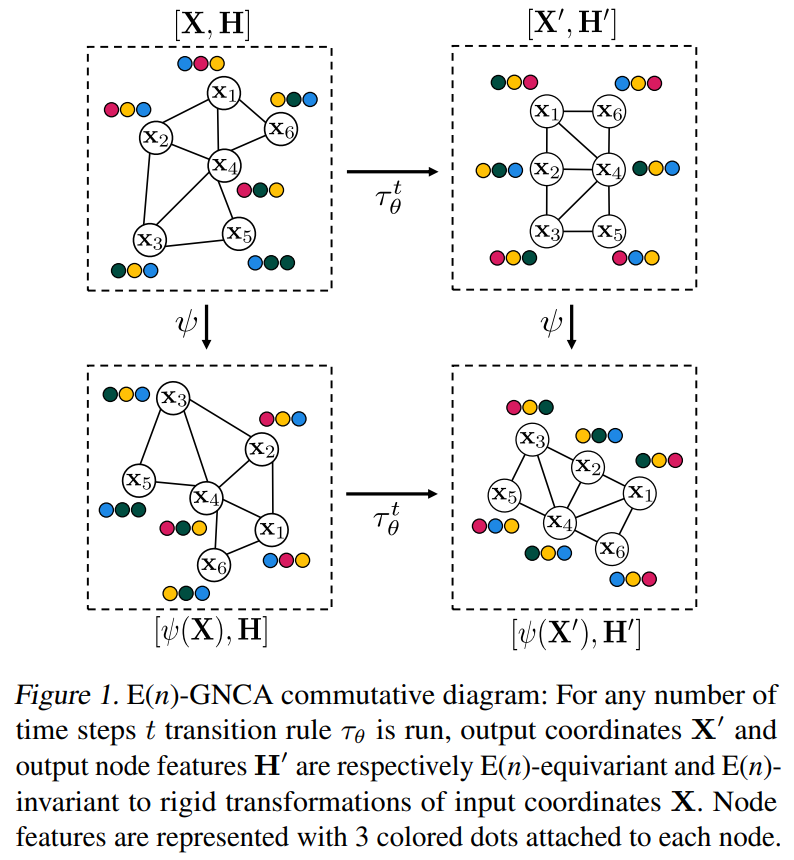
セルオートマトン(CA)は、規則的な格子状に並べられたセルの局所的な相互作用から生じる豊かな動力学を示す計算モデルである.グラフCA(GCA)は、Convolutional NNを汎用化するように、規則的な格子ではなく任意のグラフを許容することによって、標準のCAを一般化する.最近、グラフニューラルCA(GNCAs)は、任意のGCAの遷移規則を近似するように訓練できる標準のGNNの上に構築されたモデルとして提案された.既存のGNCAsは、ノードの空間的な位置の変換に対して等変ではないため、異方性である.しかし、このような変換によって関係する場合には、同一のモデルで扱われることが望ましい.E(n)-同変性のグラフ畳み込みを標準的なグラフ畳み込みに置き換えることで、設計によって異方性を回避し、E(n)-GNCAsと呼ばれる等方的自動機のクラスを提案する.これらのモデルは軽量ではあるが、大きなグラフを扱うことができ、複雑な動力学を捉え、自己組織化する行動を示すことができる.また、私たちは、パターン形成、グラフオートエンコーディング、E(n)-同変なダイナミックシステムのシミュレーションという3つの異なるタスクで、E(n)-GNCAsの広範な成功例を紹介しました.
Q&A:
Q: E(n)-GNCAとはどのようなもので、既存のGNCAとどう違うのでしょうか?
A: E(n)-GNCA は E(n)-equivariant Graph Neural Cellular Automata であり、パラメータ化された遷移ルールに単一の EGC を使用する.既存のGNCAとは異なり、大きなグラフを扱い、複雑なダイナミクスを捉え、創発的な自己組織化動作を示し、与えられた固定状態空間に収束するように設計されています.
Q: E(n)-GNCAを使用する利点は何ですか?
A: E(n)-GNCAを用いる利点は、大きなグラフを扱うことができること、複雑なダイナミクスを捉えることができること、創発的な自己組織化動作を示すことができることです.既存のGNCAとは異なり、状態空間の対称性を考慮し、ノードが隠れた状態を持つことを許容し、設計上状態空間の等角性を尊重する.
Q: E(n)-GNCAにおける創発的自己組織化行動の概念について説明してください.
A: 文脈では、E(n)-GNCAは、これらのオートマトンが示す他のタイプの行動とは異なる、創発的な自己組織化行動を示すと述べられている.しかし、これらの動作の具体的な特徴や違いは、与えられた文脈の中では言及されていない.
Q: E(n)-GNCAは、3つの課題以外にどのような応用が考えられるでしょうか?
A: E(n)-GNCAは、パターン形成、グラフ自動符号化、E(n)-不等変動力学系のシミュレーションに応用できる可能性があります.また、集合知の設計や、創発的な計算による複雑なタスクの解決にも利用できる可能性がある.さらに、その応用範囲は、自然界や技術における分散システムや自己組織化システムにも及びます.
Q: 神経遷移規則によって、システムにおける複雑な振る舞いを効率的に学習できるのはなぜか?
A: ニューラル・セルラー・オートマトンの最近の研究に見られるように、ニューラルな遷移規則を効率的に学習することで、システムにおける複雑な望ましい振る舞いを示すことができるようになります.
Q: E(n)-Equivariant Graph Convolution (EGC)とはどのようなもので、どのような性能を持つのでしょうか?
A: E(n)-同変グラフ畳み込み(EGC)は、Euclidean空間(またはEuclidean群E(n)とも呼ばれる)の対称性を考慮したグラフ畳み込みの一種です.グラフのノードに対して畳み込み演算を行い、座標、特徴、オプションの辺属性を組み込みます.メッセージの重みを順次計算し、時間によって変化する注意の重みを使用して集約します.結果として得られる出力は、スキップ接続と密なニューラルネットワークを使用して改良することができます.
Q: スキップコネクションとはどのようなもので、モデルの耐性をどのように向上させるのでしょうか?
A: スキップ接続は、グラフ・ニューラル・ネットワークにおける設計上の選択であり、深層GNNにとって非常に有益であることが証明されている.特定の層を迂回し、前の層と後の層の間で情報を直接受け渡すことができるため、モデルの回復力を向上させることができます.これにより、過剰平滑化、勾配の爆発・消失、学習の不安定性などの問題を防ぐことができます.
Q: E(n)-Equivariant Graph Convolutions with Attentionでは、注目の重みはどのように使われるのですか?
A: E(n)-Equivariant Graph Convolutionsにおける注目度とは、集約されるメッセージに異なる重みを割り当てるために使用されます.式5を式8で置き換えることで組み込まれ、各メッセージの注目度を出力する密なニューラルネットワークを使用してメッセージの重みを計算する.そして、式9で重み付けされたメッセージを用いて、ノードの特徴が集約される.
Q: 式8における密なニューラルネットワークaの機能は何か?
A: E(n)-Equivariant Graph Convolutions with Attentionの式8のdense neural networkは、メッセージmijを入力として、その注目度を出力するために使用します.これは、メッセージを集約する際に、モデルに異なる重みを割り当てる自由度を持たせるためである.
Q: 形態形成を指揮するためのシグナルメカニズムとして、hidden statesはどのように解釈されるのでしょうか?
A: E(n)-GNCAにおける隠れ状態は、形態形成をオーケストレーションするためのシグナルメカニズムとして機能します.すべてのノードは同じゲノムや遷移ルールを共有していますが、個々のノードの特徴を通じて、受信・放出・内部保存するシグナルによってコード化される情報は異なります.
Q: パターン形成タスクの目的は何ですか?
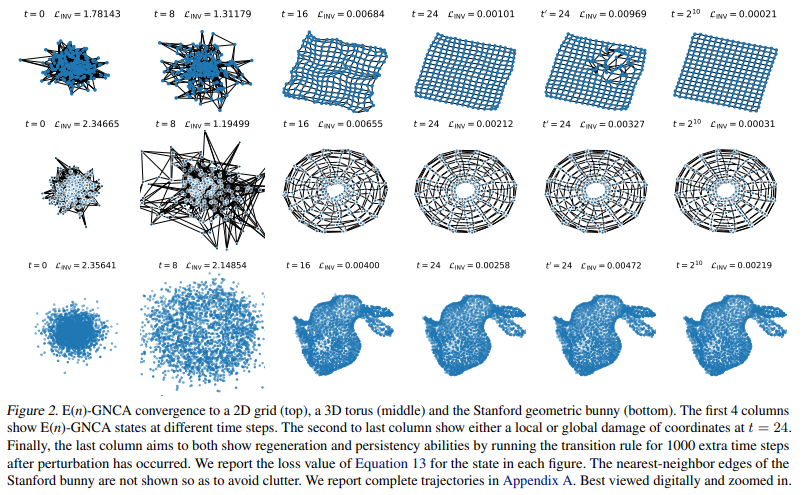
A: パターン形成タスクの目的は、ランダムに初期化された座標を、視覚的に認識可能な2Dまたは3D形状を定義する与えられたターゲットスパース幾何グラフにモーフィングするE(n)-GNCAを訓練することである.
Q: GNNの自己組織化プロセスは、外部の制御や中央集権的なリーダーの必要性を回避する方法はどのようにしていますか?
A: GNNの自己組織化プロセスは、ノードが近隣のノードとコミュニケーションをとりながら、ノードの最終的な構成について集団的な意思決定を行うものです.このプロセスは、外部からの制御や中央集権的なリーダーを必要とせず、厳密にローカルな相互作用から生じるグローバルに一貫した複雑な挙動をもたらすことができます.
Q: 式13で定義されるE(n)不変の目的語は何ですか?
A: 式13のE(n)不変の目的は、グラフのノードのすべてのペアを考慮して、モデルの最終的な構成におけるノードの各ペアの距離とターゲット点群における対応する距離の間の平均二乗誤差を最小化すると定義されています.これは、他の目的に比べて弱い監督信号を提供し、より困難なタスクとなる.
Q: 式13の最適化を行うと、どのように遷移則を学習することになるのでしょうか?
A: 式13で定義されるように、モデルの最終的な構成におけるノードの各ペアの距離とターゲット点群における対応する距離との間の平均二乗誤差を最小化することは、Grattarolaら(2021)が用いたものと比較して弱い監督信号を提供するが、モデルがターゲットのあらゆる可能な向きで収束することを可能にする.式13を最適化すると、G上で畳み込み、Xと^Xのノード間の事前1対1対応を仮定することにより、ランダムに初期化された座標Xを与えられたターゲット点群^Xにモーフィングする遷移規則を学習することになる.式13で定義される目的関数は、モデルにターゲットのあらゆる可能な方向で収束する自由を与える.
Growing Isotropic Neural Cellular Automata
著者:Alexander Mordvintsev, Ettore Randazzo, Craig Fouts
発行日:2022年05月03日
最終更新日:2022年06月01日
URL:http://arxiv.org/pdf/2205.01681v3
カテゴリ:Neural and Evolutionary Computing, Machine Learning, Cell Behavior
概要:
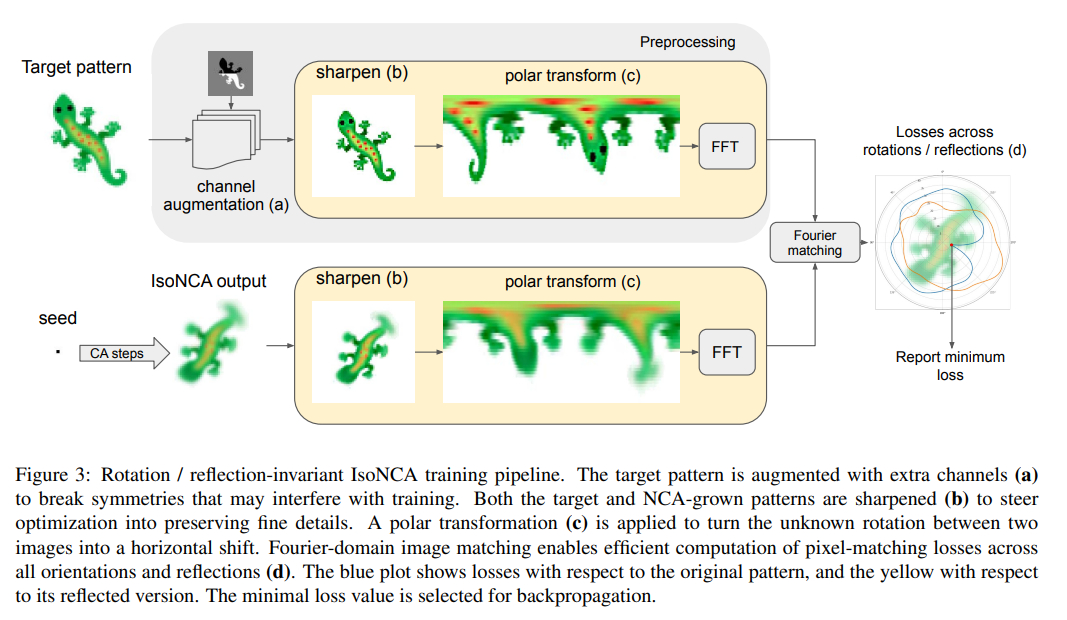
複数細胞生物が個々の細胞間の局所相互作用によって体を構築し、維持する能力を表現すること(形成)は、発生学の長年の課題である.最近、ニューラルセルオートマトン(NCA)モデルが提案され、同じ規則をグリッド上の単一のセルから反復適用することによって、指定されたグローバルビヘイビア(成長と定義済みのターゲットパターンの維持など)を生成するための局所システムルールを見つける方法として使用されている.この論文では、オリジナルのGrowing NCAモデルには重要な制限があることを指摘し、それは更新規則の異方性である.これは、細胞を特定の方向に配向させる外部要因が存在することを意味する.つまり、基礎となるシステムの「物理的」ルールは回転不変ではなく、したがって、同じグリッド上の異なる方向に向けられたターゲットパターンのインスタンスの存在を禁止する.それに対して、IsoNCAモデルを提案し、この制限がないことを示している.このような細胞系は、(1) 構造化されたシードを使用して対象性を破壊する方法または(2)非同期なセル更新によって引き起こされる対称性の破壊に依存する回転反転不変なトレーニング目的を導入することで、正確な非対称パターンを成長することができることが示されている.
Q&A:
Q: NCA(Neural Cellular Automata)モデルとはどのようなもので、どのような仕組みになっているのでしょうか?
A: ニューラルセルオートマトン(NCA)モデルは、同じルールをグリッド上の単一のセルから繰り返し適用することにより、成長し続ける指定されたターゲットパターンを生成するための局所システムルールを見つける方法です.各セルの近傍から収集された情報を入力として取る小さなニューラルネットワークによって定義されるルールを使用して、セルは状態を更新します.事前に定義されたターゲットパターンを成長させるグローバル目標を満たすローカル更新ルールを学習するために、時間をまたいで逆伝搬が使用されます.
Q: 提案されているIsoNCA(Isotropic NCA)モデルは、オリジナルモデルの制限をどのように克服しているのでしょうか?
A: オリジナルのNCAモデルには重要な制限があり、学習された更新ルールの異方性が生じます.これは、基礎となるシステムの物理的な規則が回転に不変ではないことを意味します.これにより、同じグリッド上に異なる向きのターゲットパターンのインスタンスを持つことができなくなります.提案されたIsoNCAモデルは、元のNCA更新規則の簡素化を使用して、回転に不変にすることで、この制限に対処します.つまり、各セルの認識はグリッドの回転または反射に不変です.この不変性により、IsoNCAモデルは、構造化されたシードに回転、反射、および他の拡大を実行し、予測可能にモデルの動作に影響を与えます.IsoNCAモデルには、回転反転不変のトレーニング目的も含まれており、対称性の破れによる非対称、異方性パターンの信頼性の高い成長にシステムを導くというものです.
Q: 様々な組織や生物の発生手順を説明するために、どのようなモデルが提案されているのか?
A: 様々な組織や生物の発生過程を説明するために、人工的な遺伝子制御ネットワーク(GRN)、神経細胞オートマトン(NCA)、物理的に根拠のある細胞分裂や移動のモデルなど、いくつかのモデルが提案されています.
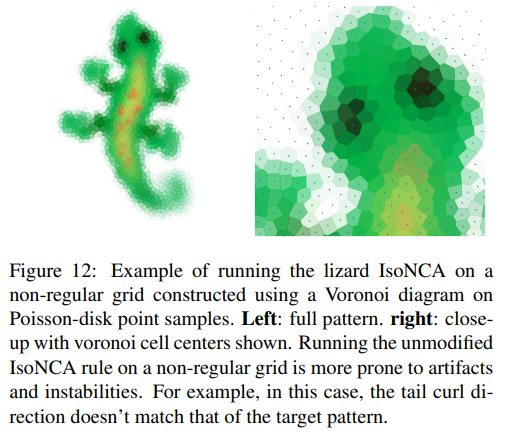
Q: Isotropic NCAモデルは、トレーニング外のグリッド構造に対してどのようにロバスト性を示すのでしょうか?
A: 等方性NCAモデルは、3×3の畳み込み知覚フィルタを6角形の対応するものに置き換えると、6角形のグリッド上で実行できるため、訓練外のグリッド構造に対する頑健性を示しています.これは、以前の研究で発見されたもので、モデルが元のトレーニンググリッド構造を超えて一般化できることを示しています.
Q: IsoNCAモデルにおいて、細胞はどのように状態を更新するのでしょうか?
A: Isotropic NCAモデルのセルは、3×3のムーア近傍から収集した情報のみを用いて、繰り返し状態を更新する.更新は確率的に行われ、各セルは確率pupdで更新される.アルファチャンネル(s3=A)は、セルが現在「生きている」のか「空っぽ」なのかを判断する上で特別な役割を果たす.
Q: IsoNCAモデルの非同期性は、対称性の破れにどのように寄与するのでしょうか?
A: IsoNCAモデルの非同期性は、細胞がパターン形成時に対称性を破るために利用できるランダム性の源となります.訓練中に、細胞は、このランダム性に依存すると思われる最終的なパターンのレイアウトを集団で決定するためのプロトコルを開発します.このランダム性は、細胞の開始条件と知覚領域の対称性を崩すのに役立ち、単一の種から回転対称でないパターンを開発することを可能にする.
Q: 細胞が「生きている」か「空っぽ」かを判断する際のαチャネルの役割を説明できますか?
A: アルファチャンネル(s3=A)は,セルが現在「生きている」か「空」かを判断する上で特別な役割を果たします.各セルは,A > 0.1 の場合,またはその3×3近傍に少なくとも1つの生きているセルがある場合に生きていると言えます.空っぽのセルの状態は、各CAステップの後に明示的にゼロに設定される.
Q: NCAモデルにおいて、あらかじめ定義されたターゲットパターンを成長させるという大目的は、どのように決定されるのでしょうか?
A: NCAモデルにおいて、あらかじめ定義されたターゲットパターンを成長させるという大目的を、時間によるバックプロパゲーションによって決定することで、既存の戦略では不可能だった、より複雑なルールの発見を可能にしました.
Q: ターゲットパターンの主要な特徴を特定のポイントにマッピングするために、構造化種子はどのように人手で操作されるのですか?
A: 構造化された種子は、ターゲットパターンの主要な特徴を種子の特定のポイントにマップするように手動で設計できます.種子の向きは、事前に定義された半径の円周上に一様に分布する3つの非共線点によって定義されます.方向の責任を確立するために、ポイントはRGBコーディングによって区別されます.トレーニング後に構造化された種子の構成を変更することで、モデルはターゲットパターンのトレーニング外の予測可能な構造変異を生じることができます.構造化された種子の構成を変更する場合は、その複合点の位置とチャネルエンコードを変更することによって行われます.
Q: 構造化シードの構成を変更すると、その合成点にどのような影響を与えるか?
A: 構造化シードの合成点の位置とチャンネルエンコーディングを変更することで、シードの構成を変更することができます.例えば、構造化シードが点Aと点Bで構成されている場合、点Aを点Bに置き換えるには、点AのRGBエンコーディングを点Bのエンコーディングに合わせることになります.
Q: 成長したパターンの向きを集団で決定するために、モデルはどのように回転対称性を壊しているのでしょうか?
A: IsoNCAモデルにおける細胞の更新の非同期性は、パターンが発達する過程で空間的な対称性を破るために細胞が依存するランダム性の源となり、最終的なパターンのレイアウトについて集団決定をすることを可能にします.このランダム性により、このモデルは確率的対称性の破れを利用し、対称的な初期条件から出発した場合でも、非対称的なパターンを生成することができる.
Q: 学習済みモデルが生成したパターンをターゲットにマッチングさせる際のピクセル単位の差分の概念を説明できますか?
A: ピクセル単位の差分という概念は、学習済みモデルが生成したパターンをターゲットに一致させるために、すべての半径値およびターゲットチャンネルにわたって、NCAが生成したパターンとターゲットとのピクセル単位の差分の二乗和を最小化するものです.これは、回転反射不変の損失関数を使用して行われます.
Q: グローイングNCAの作品は、シングルシード戦略とどう違うのですか?
A: Growing NCAとSingle-seed戦略は、どちらも1つのシードセルから始まる平面上の事前定義されたパターンを成長させ、持続させるためにNCAモデルをトレーニングします.しかし、Single-seed戦略は、回転反射に影響されないように損失関数を変更し、トレーニング中に特定のパターンの方向とキラリティを強制しません.一方、Growing NCAには異方性の制限があり、学習された更新ルールは回転に不変ではないため、同じグリッド上に異なる向きのターゲットパターンのインスタンスが存在することを禁止していることを意味しています.
Q: 本稿で紹介した方法は、従来の方法と比較してどのようなメリットがあるのでしょうか?
A: 今回紹介する論文は、Malheirosらによる「The Leopard Never Changes Its Spots:この新しい方法は、等方性ニューラルセルラーオートマトン(IsoNCA)モデルを改良したものです.新手法が旧手法と比較して特に優れている点は、同じグリッド上に同じターゲットパターンの複数のインスタンスを生成できないという制約がないことである.
Q: 本論文の実用的な貢献は何ですか?
A: 「Growing Isotropic Neural Cellular Automata」と題された論文の実用的な貢献は、回転-反射不変で、外部からの誘導ではなく対称性の破れによって非対称で異方性のパターンの成長を可能にする修正アイソトロピックNCA(IsoNCA)モデルの提案、学習グリッド構造に対するNCAルールの頑健性の実証です.このモデルは、構造化されたシードに対して、回転、反射、その他の補強を行うことができ、モデルの挙動に影響を与えることが予測されます.
Q: 本論文の理論的な貢献は何ですか?
A: 「Growing Isotropic Neural Cellular Automata」という論文の理論的貢献には、元のGrowing NCAモデルを等方性にするための修正の提案、回転反射不変トレーニング目的の設計、学習されたNCAルールのトレーニング外グリッド構造に対する堅牢性のデモンストレーションが含まれます.さらに、著者らは等方性NCA(IsoNCA)モデルが、予測可能な方法でモデルの動作に影響を与える構造化シードの回転、反射、およびその他の拡張を可能にすることを示しています.
Q: 実験やデータ解析で得られた主な知見は何ですか?
A: 本論文では、オリジナルのGrowing Neural Cellular Automata (NCA)モデルには、そのアーキテクチャに限界があることを論じている.学習した更新ルールは異方性であり、これは基礎システムの物理ルールが回転に対して不変でないため、同じグリッド上に異なる方向のターゲットパターンのインスタンスを形成することを禁止していることを意味する.本論文では、この制限に対処し、細胞を特定の方向に向けるための外的要因を必要としない、修正アイソトロピックNCA(IsoNCA)モデルを提案する.主な発見は、IsoNCAモデルが回転不変で、同じグリッド上に複数の方向で存在できるパターンを生成できることである.
Goal-Guided Neural Cellular Automata: Learning to Control Self-Organising Systems
著者:Shyam Sudhakaran, Elias Najarro, Sebastian Risi
発行日:2022年04月25日
最終更新日:2022年04月25日
URL:http://arxiv.org/pdf/2205.06806v1
カテゴリ:Neural and Evolutionary Computing, Machine Learning
概要:
神経細胞オートマトン(NCAs)は、細胞成長と自己組織化に触発され、人工細胞をイメージ、3D構造、さらには機能的な機械にまで成長させることができる.NCAsは柔軟で頑強な計算システムであるが、多くの他の自己組織化システムと同様に、成長プロセス中および後に本質的に制御できない.本研究では、Goal-Guided Neural Cellular Automata(GoalNCA)と呼ばれる、ゴール符号化を活用して細胞の動作を成長の各段階で動的に制御するアプローチを紹介する.このアプローチにより、NCAは常に動作を変更し、場合によっては未知のシナリオに対して動作を汎化することができる.また、わずかな細胞がゴール情報を受信した場合でも、タスクパフォーマンスを維持するNCAの堅牢性も示している.
Q&A:
Q: ニューラル・セルラー・オートマトン(NCA)とは何か、どのような仕組みなのかを説明してください.
A: ニューラル・セルラー・オートマトン(NCA)は、コンパクトなニューラルネットワークと細胞の状態を用いて、目的関数に導かれながらローカルルールを学習しようとする計算システムである.各細胞はベクトルとして表現され、ターゲットチャンネル、細胞が生きているか死んでいるかを決定するリビングチャンネル、そして一種の細胞記憶として機能する隠れチャンネルで構成されています.NCAは、小さな「生きた」細胞の集合、すなわち「種」から始まり、やがて時間とともに完全な人工生物に成長する.NCAは、2D画像や物理的な2D形状の自己分類、ゲームのレベル、再生機能付き3Dマシンなど、さまざまなタスクの学習に有効であることが示されている.
Q: 人工細胞を画像や3D構造、機能的な機械に「成長」させるために、NCAはどのように利用されているのでしょうか?
A: ニューラル・セルラー・オートマトン(NCA)は、コンパクトなニューラルネットワークと細胞の状態を用いて、目的関数に導かれながらローカルルールを学習しようとするものです.通常、NCAは小さな「生きた」細胞の集合(「種」)から始まり、やがて完全な人工生物に成長します.NCAは、人工細胞を画像や3D構造、さらには機能的な機械に「成長」させることが可能です.
Q: NCAの学習は、どのようなプロセスで、多様なモノを育てることにつながるのでしょうか?
A: NCAの学習プロセスは、初期の「生きた」細胞や「種」の小さなセットから始まり、最終的には時間をかけて完全な人工生物に成長します.初期シードは静的なベクトルであることもあれば、単一のNCAネットワークから多様なオブジェクトのセットを成長させるように学習させることもできます.
Q: 提案されたバリエーションであるGoalNCAは、多くの独立したコンポーネントからなる自己組織化システムを制御するという課題にどのように対処するのでしょうか?
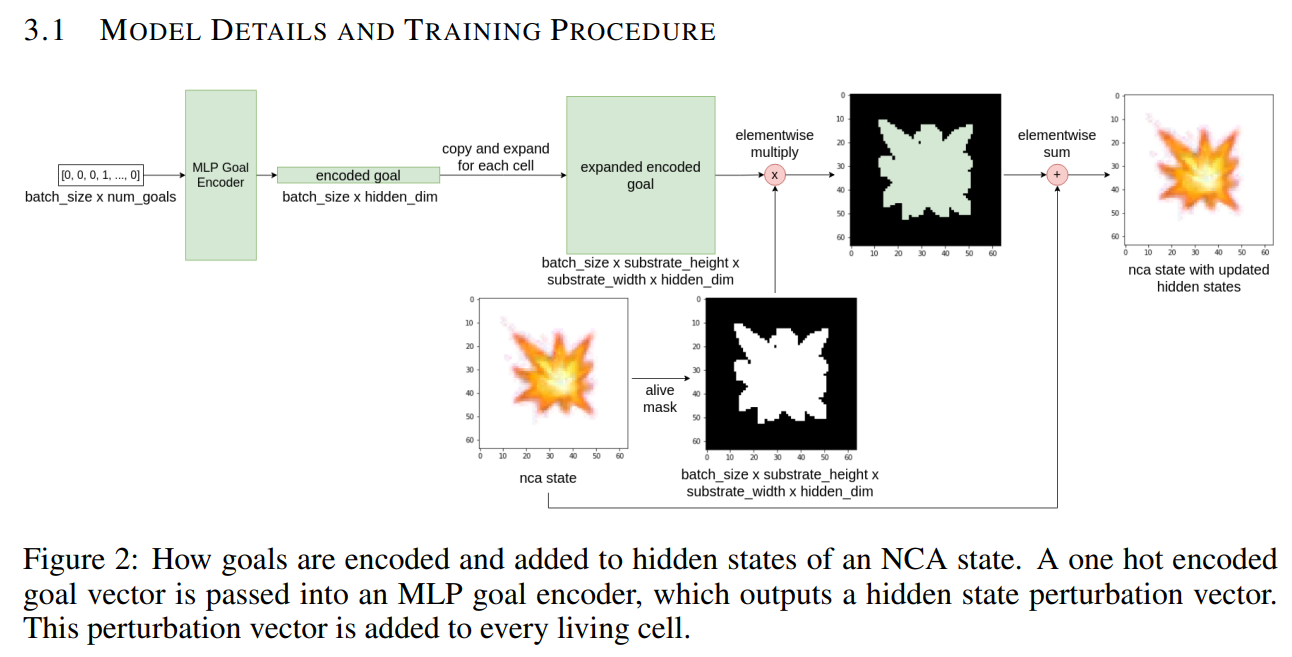
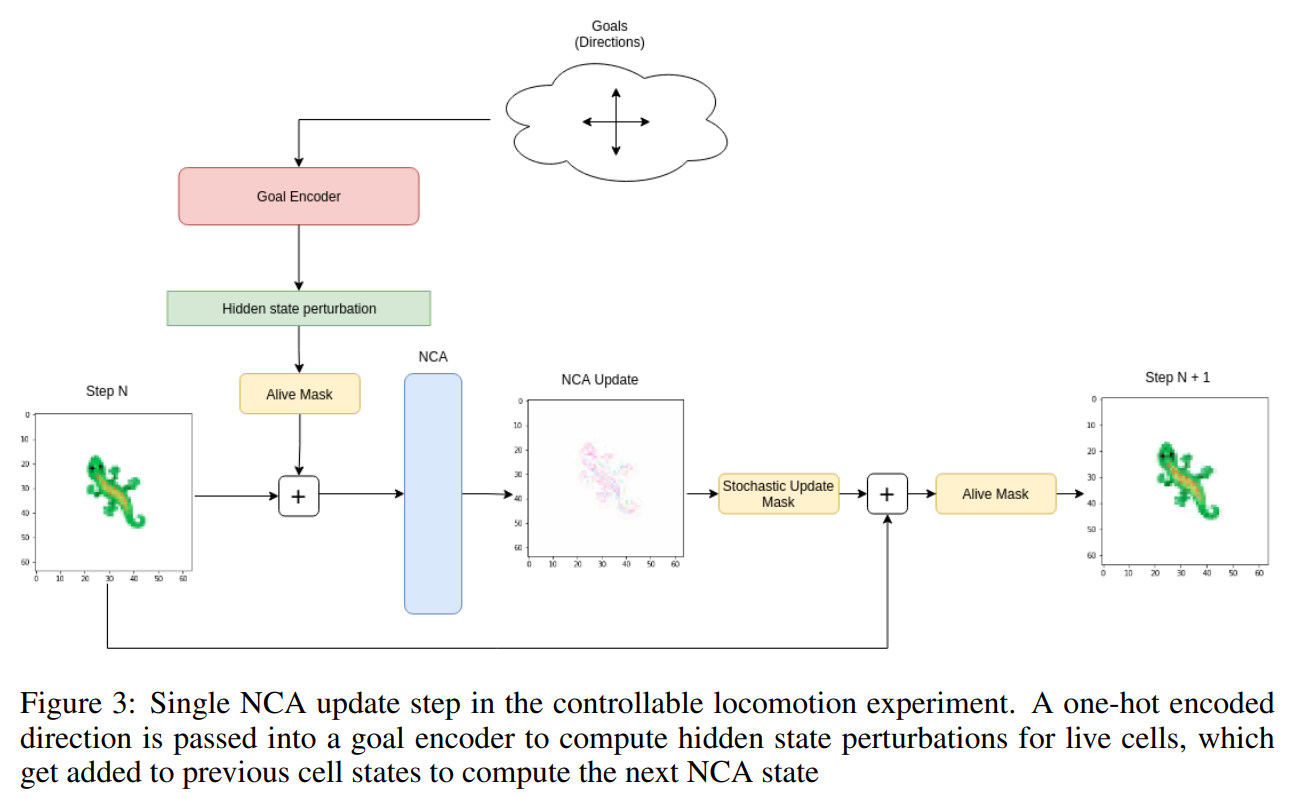
A: GoalNCAは、目標を導くためのエンコードされた目標ベクトルを使用して細胞を誘導し、成長中に細胞の振る舞いを動的に変更する、自己組織化システムを制御するアプローチです.これにより、多数の独立したコンポーネントから構成される自己組織化システムを制御するという課題に対応し、NCAを継続的に振る舞いを変更し、一部の場合には未知のシナリオに対して振舞いを一般化する能力を提供します.提案されたアプローチは、成長サイクルの各ステップで全ての生き残った細胞の隠れ状態を更新し、驚くべきことに、これらの簡単な追加は、画像の形態変形や運動力学の学習などのタスクに向かった細胞振る舞いを誘導するのに効果的であるという点であります.
Q: NCAで得られた知見は、自己組織化システムをより制御しやすくするためにどのように役立つのでしょうか?
A: NCAで得られた知見は、自己組織化システムをより制御しやすくするために、細胞の一部だけが目標情報を受け取っていても誘導できることを示したり、情報が欠落した不完全な環境でも繁栄できるように、自己組織化システムの動的挙動を開発したりするのに役立つと考えられます.これは、将来の興味深い研究の方向性を開くものである.
Q: 提示されたアプローチの主な貢献は何ですか?
A: Goal-Guided Neural Cellular Automata (GoalNCA)と呼ばれる本アプローチの主な貢献は、目標エンコーディングを活用して、細胞成長の各ステップで細胞の行動を動的に制御し、システムが継続的にその行動を変更し、未知のシナリオに対してその行動を一般化できるようにしたことである.また、このアプローチでは、一部の細胞だけがゴール情報を受け取った場合でも、タスクのパフォーマンスを維持することができ、NCAの頑健性を実証しています.
Q: 本稿で紹介した方法は、従来の方法と比較してどのようなメリットがあるのでしょうか?
A: 本論文では、自己組織化システムを制御し、画像のモーフィングや運動ダイナミクスの学習といったタスクに向けて細胞の挙動を誘導するアプローチとして、Goal-Guided Neural Cellular Automata (GoalNCA) を紹介する.GoalNCAの利点は、目標エンコーディングを活用して、細胞成長の各ステップで細胞の行動を動的に制御することで、NCAが継続的に行動を変化させ、未知のシナリオに対してその行動を一般化することができることです.また、GoalNCAは、一部の細胞だけがゴール情報を受け取った場合でも、タスクのパフォーマンスを維持することで、ロバスト性を実証しています.一方、従来の自己組織化システムでは、成長過程終了後の細胞の柔軟性や制御性に欠けていました.
Q: 新方式を実現するために必要な計算資源はどのくらいですか?
A: 論文では、GoalNCAアプローチは、両方の実験において、2k以下のパラメータを持つ小さな線形ゴールエンコーダを追加で必要とするだけだと述べています.
Q: 本論文の実用的な貢献は何ですか?
A: 本論文で紹介したゴールガイド・ニューラル・セルラー・オートマトンのアプローチは、ゴールエンコーディングによる自己組織化システムの制御、細胞成長の各段階における細胞の行動の動的ガイド、NCAの継続的な行動変化、場合によっては未知のシナリオへの行動一般化などの実用的貢献を果たしています.また、このアプローチでは、一部の細胞のみが目標情報を受け取った場合でも、タスクのパフォーマンスを維持することができ、NCAの頑健性を実証しています.
Q: 本論文の理論的な貢献は何ですか?
A: 論文で紹介したGoal-Guided Neural Cellular Automataアプローチの理論的な貢献としては、ゴールエンコーディングを用いて自己組織化システムを制御する能力、細胞成長の各ステップで細胞の挙動を動的に変更する能力、細胞の一部だけがゴール情報を受け取った場合でもタスクパフォーマンスを維持することが挙げられます.さらに、このアプローチにより、NCAは継続的に挙動を変化させ、未知のシナリオに対してその挙動を一般化することができる.
Q: 実験やデータ解析で得られた主な知見は何ですか?
A: この論文の主な成果は、自己組織化システムを制御するための目標誘導型ニューラルセルラーオートマトン(GoalNCA)アプローチを開発し、NCAが継続的に行動を変化させ、未知のシナリオに対して行動を一般化できるようにしたことです.このアプローチでは、目標エンコーディングを活用して、細胞成長の各ステップで細胞の挙動を動的に制御します.また、一部の細胞だけが目標情報を受け取った場合でも、タスクのパフォーマンスを維持することができ、NCAの頑健性を実証しています.モデルは、シンプルな3層MLPゴールエンコーダと、Mordvintsev et al.(2020)で提案されたものと同様の典型的なNCAで構成されています.


コメント