機械学習/深層学習などの分野を勉強するさい、講座や教科書でもあまり言及されることがない用語、「帰納バイアス」.しかし、論文ではよく使われる用語で、近年の機械学習モデルの精度の発展を理解するのに欠かせない概念です.もはや、これなしに現在のAIの発展は語れないとも言えると思います.
帰納バイアスを一言でまとめると、未知のデータに対して正しく推論できる関数(汎化する関数)が学習されやすいように設ける、データに関すること前知識や仮定に基づいた「モデルの学習可能な関数への制約」であると言えます.
機械学習モデルは様々な関数を学習することが可能です.モデルによっては、十分なパラメータ数が設けられれば万能近似によって、どんな関数でも学習可能なことが保証されています.
学習に使われる訓練データは標本分布であり、それらのデータにフィットする関数(目的関数を最小化する関数)が無数に存在します.その中で、訓練データにはない、母集団からの未知のデータへ正しい推論を行える関数はごく少数なので、高確率で汎化しない関数が導かれます.そこで、母集団に関する知識を用いて制約をあたえて、学習される関数を汎化しやすいものに絞ってあげることで、より高い確率で汎化する関数を導くことができます.
この制約に使われること前知識は大まかに以下の特徴量と入力データの2つのドメインに分けることが出来きます.
1.特徴量上の仮定の例
- 決定境界の形.例:線形決定境界のロジスティクス回帰、Linear SVM.
- 基盤となる確率分布.例:複数の多変量正規分布からなるGaussian Mixture Model (GMM)
2. 入力データ上の仮定の例
- 受容野 (Receptive Field). 例:CNNのフィルターの局所性
- 対称性 (Symmetry). 例:Transformerの置換変換に対しての同変性
学習可能な関数の集合を\( \small \mathcal{F}=\{f:X \rightarrow Y\} \)としましょう.データの目的関数は損失関数、\( \small \frac{1}{N} \displaystyle\sum_{i=1}^N \mathcal{L}(f(x_i),y_i) \) として、それを最小化にするのが訓練データの学習とします.
集合\( \small \mathcal{F} \)の中で損失を最小化する関数は膨大に存在しますが、その中で訓練データにはない未知のデータに対して正しく推論できる汎化する関数はごくわずかとなるので、学習時にそのような関数にたどり着く確率はかなり低いと言えます.一方で、関数空間を適切な帰納バイアスで絞れば損失を最小化する関数の集合は縮小し汎化する関数の集合に近づくため、汎化する関数にたどり着く確率が上がります.
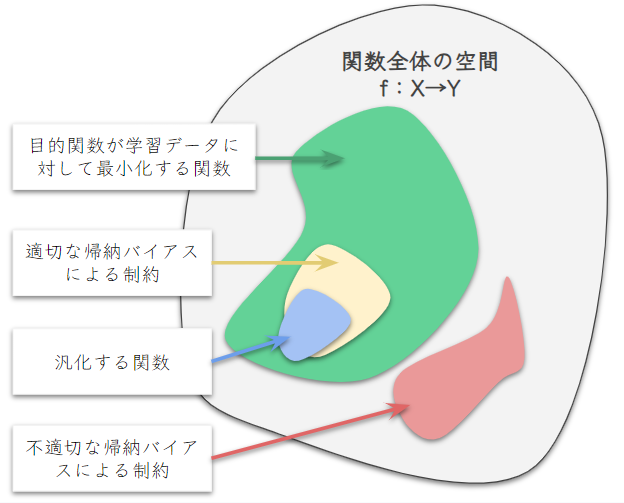
しかし、問題点はそのデータに適切でない帰納バイアスを用いてしまった場合、汎化する関数が学習される可能性がゼロ、もしくはかなり低くなってしまうので帰納バイアスの選択は入念な注意が必要です.
決定木 (Decision Tree) と深層学習 (DNN)の等価性と帰納バイアス
例として決定木と深層学習をの帰納バイアスを比較します.これらのモデルの学習方法は異なりますが、学習される関数に等価性があります(※ReLU活性化関数などを深層学習に用いた場合).[1]では、深層学習でのフィードフォワード処理と同等な決定木を描くことで、行列変換+決定木が深層学習と等価していることが示されています.
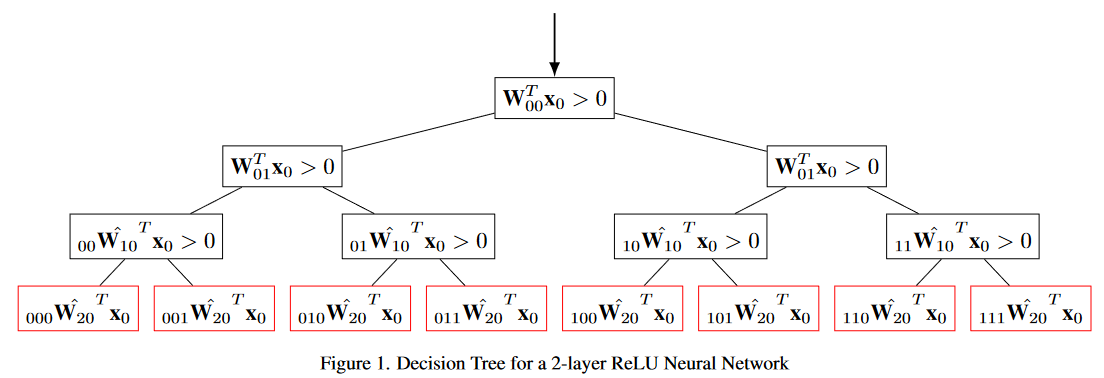
\( \small \mathbf{x}_{0} \)内の一つの要素が出力されるような行列変換を選べば、決定木アルゴリズムと同等になります.つまり、決定木アルゴリズムが学べる関数は全てニューラルネットワークでも学べることになるので、学べる関数の集合の大きさを比較すると、\( \small \mathcal{F}_{決定木}\subset \mathcal{F}_{深層学習} \)、となります.よって深層学習の方が帰納バイアスが弱いことが分かります.
State Of The Art (SOTA) と帰納バイアス
なぜ冒頭で述べたように、帰納バイアスが重要な概念であるかというと、近年のAIモデルの精度の競い合いは、大半が帰納バイアスの競い合いと考えられるからです.モデル精度向上の典型的なレシピは、帰納バイアス緩和+学習データの増加、であり、これが繰り返し行われてきて徐々に精度が向上されてきました.
例として、近年の大規模言語で大活躍しているTransformerは帰納バイアスが比較的弱いネットワークです.画像系でよく使われる、Convolutional Neural Network (CNN)と比べても大分弱い帰納バイアスを持っています.今では、画像分類タスクでもTransformer系のネットワーク、Vision Transformer (ViT) が上位を占めています.
CNNやTransformerの帰納バイアスを比較するには、Graph Neural Nework の観点が便利です.詳しくは、「Graph Neural Network によるモダンネットワークの一般化」で解説していますので、良ければそちらをご覧ください.
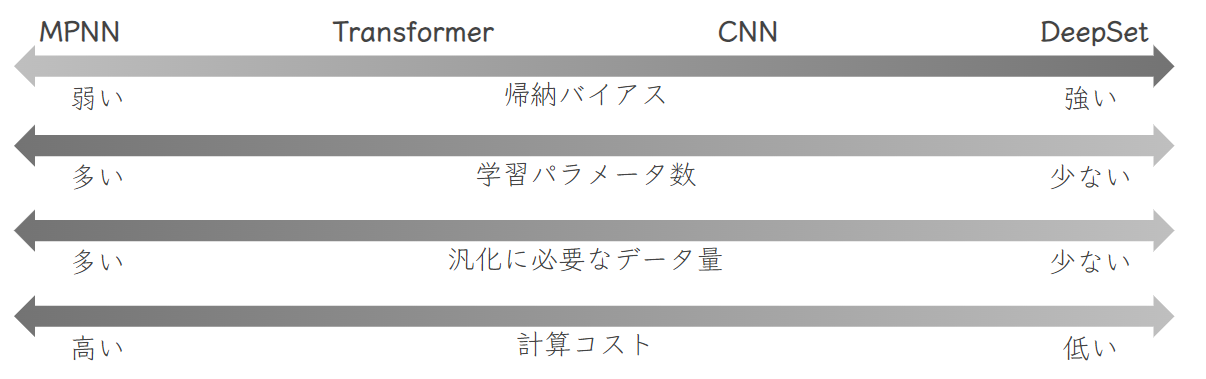
Transformer以上に帰納バイアスが弱いネットワークの例は Message Passing Neural Network (MPNN) です.これまでの、精度向上のレシピを鑑みると、いつかはTransformerより帰納バイアスが弱いネットワークが主流になる日が来るかもしれませんね.
しかし、このレシピによる精度向上は、その都度より高い計算資源とデータ量が求められ、今では、Google、Microsoft社などの膨大なデータと計算資源を誇る大企業でしか、SOTAは達成しにくくなっているのが現状でしょう.色々工夫して、「最強のAIを作ってやる!」っと意気込みの強いAIエンジニア/研究者にとっては、残念ながら高いコストをかけて良い結果を出しても、すぐにより膨大な計算資源とデータ量の数の暴力によって記録が塗り替えられてしまうので、無駄な努力に終わる可能性が高いのです.
モデルと帰納バイアスのリスト
| モデル | 帰納的バイアス |
|---|---|
| 線形回帰 | 属性\( \small x \)と出力\( \small y \)との関係は線形.目標は二乗誤差の合計を最小化すること. |
| 決定木 | 古典的な決定木アルゴリズムであるID3アルゴリズムは、長い木よりも短い木を好み、情報利得が高い属性をルートに近い位置に配置する |
| K-最近傍法 | 特徴空間で近接するケースが同じクラスに属する傾向があるという仮定. |
| サポートベクターマシン (SVM) | 別々のクラスは、広い余白(マージン)で区切られる. |
| ナイーブベイズ | それぞれの入力は出力クラスまたはラベルだけに依存し、入力値は互いに独立している. |
| バックプロパゲーションによる深層学習 | データポイント間の滑らかな補間. ReLUなどの活性化関数を用いた場合、スプライン理論では入力空間がラゲールボロノイ図になる. |
| DeepSet | 置換変換群\( \small S_n \)の作用の同変写像 |
| Convolutional Neural Network (CNN) | 並進変換群\( \small (\mathbb{R},+) \)の作用の同変写像 局所性 |
| Transformer | 置換変換群\( \small S_n \)の作用の同変写像 |
| Normalizing Flow | データ分布を近似する可微分多様体の微分同相写像 |
まとめ
- 帰納バイアスは、未知のデータに対して正しく推論できる関数が学習されやすいように設けるための制約である.
- 決定木と深層学習の帰納バイアスを比較すると、深層学習の方が帰納バイアスが弱いことが分かる.
- 近年のAIモデルの精度の競い合いは、大半が帰納バイアスの競い合い、帰納バイアスの緩和と学習データの増加がモデル精度向上の典型的なレシピである.
- 近年の大規模言語で活躍しているTransformerは、帰納バイアスが比較的弱いネットワークである.
- Graph Neural Networkの観点から見ると、CNNやTransformerよりも帰納バイアスが弱いネットワークであるMessage Passing Neural Network (MPNN) が存在する.
- 精度向上のためには高い計算資源とデータ量が必要であり、大企業でしかSOTAを達成することが難しいくなってきている.
参考文献:
[1] C. Aytekin, “Neural Networks are Decision Trees.” arXiv, Oct. 25, 2022. Accessed: Nov. 05, 2022. [Online]. Available: [http://arxiv.org/abs/2210.05189](http://arxiv.org/abs/2210.05189)