はじめに
近年、深層学習が画像認識や自然言語を含めた様々なドメインで活躍しています.代表的なネットワーク構造として、Convolutional Neural Network (CNN) や Transformerなどが挙げられますが、今回は、これらはGraph Nerural Network (GNN) という、より大きな枠組みの一つであると言う話です.
結論から言うと、GNNの枠組みにより構造が全く異なると思われがちなCNNとTransformerの共通点が明確になります.Convolutional Neural Netowork (CNN)|CNNの学習可能な関数空間を拡張して、より幅広い関数の学習がTransformerによって可能になた事が自然な形で分かります.Bias vs. Variance Trade-offの観点から見ると、関数空間への制約(帰納的バイアス)をよりリラックスさせることで、より複雑な変数の関係性が学習できる反面、過学習しやすく多くのデータが必要になるのがTransformerです.よくTransformerの方がCNNより優れているようなニュアンスで書かれている記事を見かけますが、これは誤った認識で厳密にはタスクやデータ量に依存します.データ量が増えるにつれ、学習可能な関数空間を広げることで精度を徐々に高くしていった【 CNNベースのResNet 】 ➡ 【 TransformerベースのViT 】 ➡ 【全結合ベースのMLP-Mixer 】という画像認識の経歴もあるので〇〇が一般的に優れているように印象付けられてしまいがちです.
Graph Neural Networks (GNN)
ここでは、簡単にGNNの中でもSpatialタイプという類で代表的なMessage Passing Neural Network (MPNN) の演算を紹介してCNNやTransformerなどのネットワークと比較していきます.まずは、グラフ \( \small G=(V,E) \)を考えます.ここで、\( \small V, E \) はそれぞれグラフのノード (vertex) とエッジ (edge) です.画像や自然言語のデータをグラフに当てはめるイメージが湧きにくいですが、画像の場合は各ピクセルで自然言語では各トークンがノードとなります.エッジはネットワークの順伝播するさいに、各ノードに対してどのノードたちを近傍とするかを定義します.CNNの場合は、各ピクセルに対してフィルターの内積に含まれる周りのピクセルを近傍とするので、それらとエッジが繋がるイメージです.Transformer内のSelf-Attention、またはCross-Attentionでは、各トークンに対して他の全てのトークンを演算に含めるため各ノードが全てのノードとエッジによって繋がる完全グラフとなります.
各ノードが持つ情報は\( \small d \)次元のベクトルで表され、例えばノード \( \small v \) の入力ベクトルを\( \small \mathbf{x}_v \in \mathbb{R}^{d } \)とし、\( \small \mathbf{h}^{(l)}_{v}\in \mathbb{R}^{d^{(l)}} \) を\( \small l \)番目の層の潜在ベクトルとします.ただし、\( \small d^{(0)}=d \)とします.畳み込みネットワーク (CNN) では、チェンネル数をベクトルの次元数と考えると特徴マップが画像上のベクトル場と見ることができます.それらが各層で算出されていくイメージと同様に、ここではグラフ上のベクトル場が各層で算出されていきます.
Message Passing Networks (MPNN)
MPNNの処理を明示すると以下の手順で算出されていきます. $$ \small \mathbf{h}^{(0)}_v = \mathbf{x}_v, \ \ \forall v \in V \tag{初期化}$$ $$ \small
\begin{equation}
\begin{split}
\mathbf{m}^{(l)}_u &=\displaystyle\bigoplus_{v \in \mathcal{N}_u}\mathbf{m}^{(l)}_{uv}\ \\ &= \displaystyle\bigoplus_{v \in \mathcal{N}_{u}}\phi_1^{(l)}(\mathbf{h}^{(l-1)}_u,\mathbf{h}^{(l-1)}_{v},\mathbf{e}_{uv})
\end{split}
\end{equation}
\tag{メッセージの集計}
$$ $$ \small \mathbf{h}_u^{(l)} =\phi_2^{(l)}(\mathbf{h}_u^{(l-1)},\mathbf{m}_{u}^{(l)})\tag{更新}$$
ここで、\( \small \mathcal{N}_v \)はノード \( \small v \) を含めた \( \small v \) の隣接ノードたちの集合.
\( \small \displaystyle\bigoplus_{v \in \mathcal{N}_v} \) は任意の置換不変な演算子であり例としては総和, \( \small \displaystyle\sum_{v \in \mathcal{N}_v} \) や最大値などが挙げられます.
\( \small \mathbf{e}_{uv} \) はグラフエッジの特徴ベクトル、\( \small \phi_1 \) や\( \small \phi_2 \)は学習される任意の関数ですが典型的には以下の型となる全結合層が使われます. $$ \small \phi_{i}(\mathbf{x}_1,\mathbf{x}_2,…,\mathbf{x}_{n})= \mathbf{W}^{(M)}\sigma(…\sigma(\mathbf{W}^{(2)}\sigma(\mathbf{W}_1^{(1)}\mathbf{x}_1+\mathbf{W}_2^{(1)}\mathbf{x}_2+…+\mathbf{W}_n^{(1)}\mathbf{x}_n+\mathbf{b}^{(1)} )+\mathbf{b}^{(2)})…+ \mathbf{b}^{(M)}$$
Graph Attention Networks (GAT)
次はMPNNの一般的な型から特殊ケースを定義していきます.今度は、エッジ特徴ベクトル\( \small e_{uv} \)は省き、隣接ノードとの関係を上記のベクトルによるメッセージ \( \small \mathbf{m}^{(l)}_{uv} \) という形式から、より表現力の低いスカラー値関数 \( \small a:\mathbb{R}^{d^{(l-1)}}\times\mathbb{R}^{d^{(l-1)}} \rightarrow \mathbb{R} \) に置き換えます.この関数をAttention関数と呼びます.そしt、上記のメッセージ集計ステップでの\( \small \phi^{(l)}_1 \)関数を以下のものに置き換えたものが Graph Attehtion Network (GAT) と呼ばれます. $$ \small \phi^{(l)}_1 = a(\phi_{\text{query}}(\mathbf{h}^{(l-1)}_u),\phi_{\text{key}}(\mathbf{h}^{(l-1))}_v)\phi_{\text{value}}(\mathbf{h}_v^{(l-1)}) \tag{1}$$
\( \small a \)は任意の関数ですが、一般的にベクトルどうしの類似度を計るカーネル関数\( \small \kappa \)を用いて以下で定義されます. $$ \small a(\mathbf{q}^{(l-1)}_u,\mathbf{k}^{(l-1)}_v) = \frac{\kappa(\mathbf{q}^{(l-1)}_u,\mathbf{k}^{(l-1)}_v)}{\displaystyle\sum_{v \in \mathcal{N}_v}\kappa((\mathbf{q}^{(l-1)}_u,\mathbf{k}^{(l-1)}_v)}$$ TransformerなどでのSelf-Attentionで使われるカーネル関数は指数カーネル(exponentiated karnel)で、それによって\( \small a \) はSoftmax関数となります. $$ \small a(\mathbf{q}^{(l-1)}_u,\mathbf{k}^{(l-1)}_v) = \text{Softmax}(\mathbf{q}^{(l-1)}_u,\mathbf{k}^{(l-1)}_v)$$ ここで、\( \small a \) が非負であることと\( \small \displaystyle\sum_{v \in \mathcal{N}_v}a(\mathbf{q}^{(l-1)}_u,\mathbf{k}^{(l-1)}_v) = 1 \)であることに注意すると、GATでのメッセージ集計ステップでは、\( \small \{\phi_{\text{value}}(\mathbf{h}_v^{(l-1)})\}_{v \in \mathcal{N}_{v}} \)によって形成される凸包 (convex hull) 内のベクトルが出力となることが分かります.そして、Transformerはメッセージをスカラーに絞ったMPNNの特殊ケースであることがこれまでの成行きから分かると思います.
Graph Convolutional Networks (GCN)
GATで隣接ノードとの情報に扱ったスカラー関数にさらなる制約を課して、
\( \small a(\mathbf{h}^{(l-1)}_u,\mathbf{h}^{(l-1)}_v) \)をベクトル変数に依存しない学習可能な係数 \( \small c_{uv} \) で以下の用に置き換えたものがGraph Convolutional Network (GCN) となります. $$ \small \phi^{(l)}_1 = c_{uv}\phi_3(\mathbf{h}_v) \tag{2}$$
ここで重要なのは、GCNはGATの特殊ケースであり、入力ベクトルによらず常に一定の値を返すようなAttention関数がGATで学習されれば、GATのモデルもGCNのモデルと等価することとなります.つまり、GCNで学習できる関数は全てGATでも学習が可能ということです.
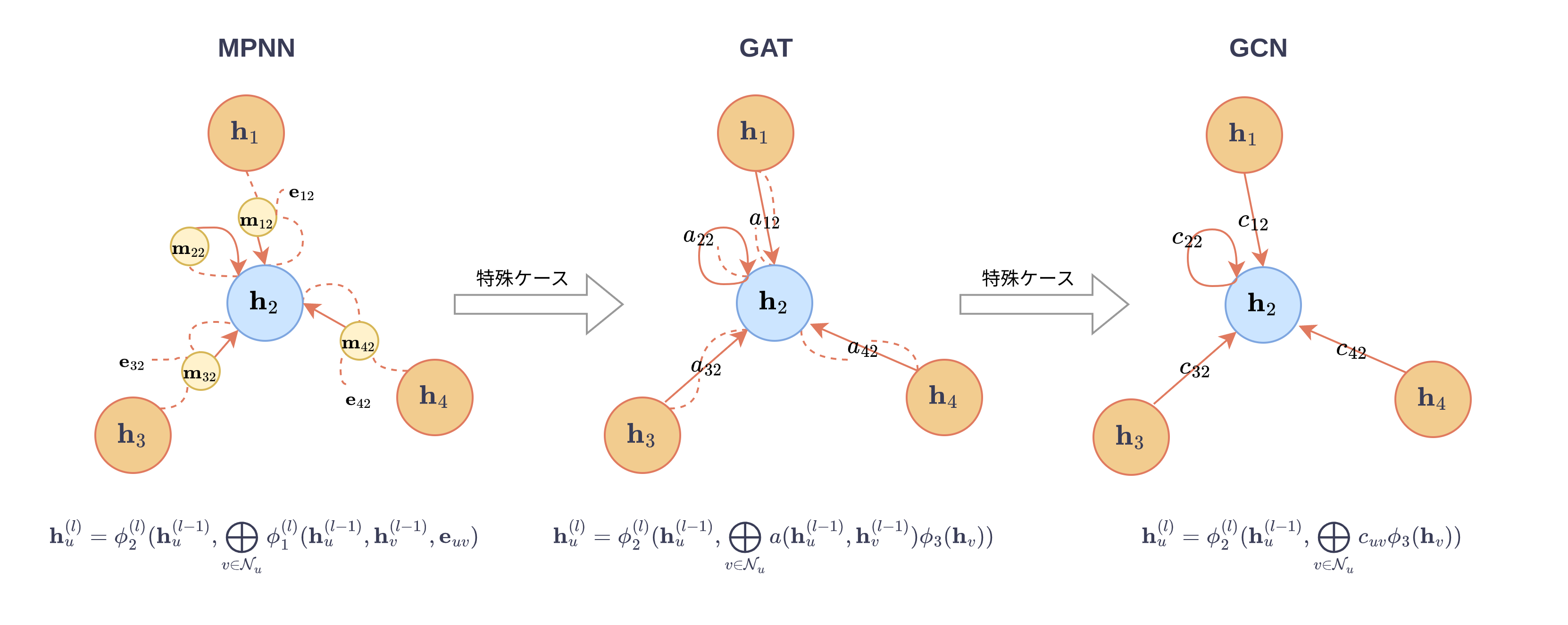
グラフ\( \small G \)がグリッド状になったGCNは2次元CNNと同じです.完全グラフを用いたGCNを用いると、CNNでのグリッド状のグラフが完全グラフの部分グラフであるため適切な係数\( \small c_{uv} \)が0になるように学習されれば、完全グラフのGCNもCNNと同じ関数を学習できます.つまり、上位グラフを用いたネットワークはその部分グラフのモデルで学習できる関数を全て学習することが可能です.
学習可能な関数空間の比較
まず学習可能な全ての関数の空間 Space of All Learnable Functions, \( \small \mathbb{F} = \{ \mathcal{F}: \mathcal{X} \rightarrow \mathcal{Y}\} \) を考えます.そして、各ネットワークの枠組みで学習可能な空間を考えると以下のような順序が付けられるます. $$ \small \mathbb{F}_{\text{GCN}}\subset \mathbb{F}_{\text{GAT}}\subset \mathbb{F}_{\text{MPNN}}\subset \mathbb{F}_{\text{spatial}}\subset \mathbb{F}$$ 関数空間が大きくなればなるほど、より多くの関数から選択することができるので、よりデータに適合しやすくなる一方、それらを検索するコストや汎化するために必要なデータ量が上がります.CNN,RNN,Transformerなどのモダンネットワークを含めると以下の図のようになります.
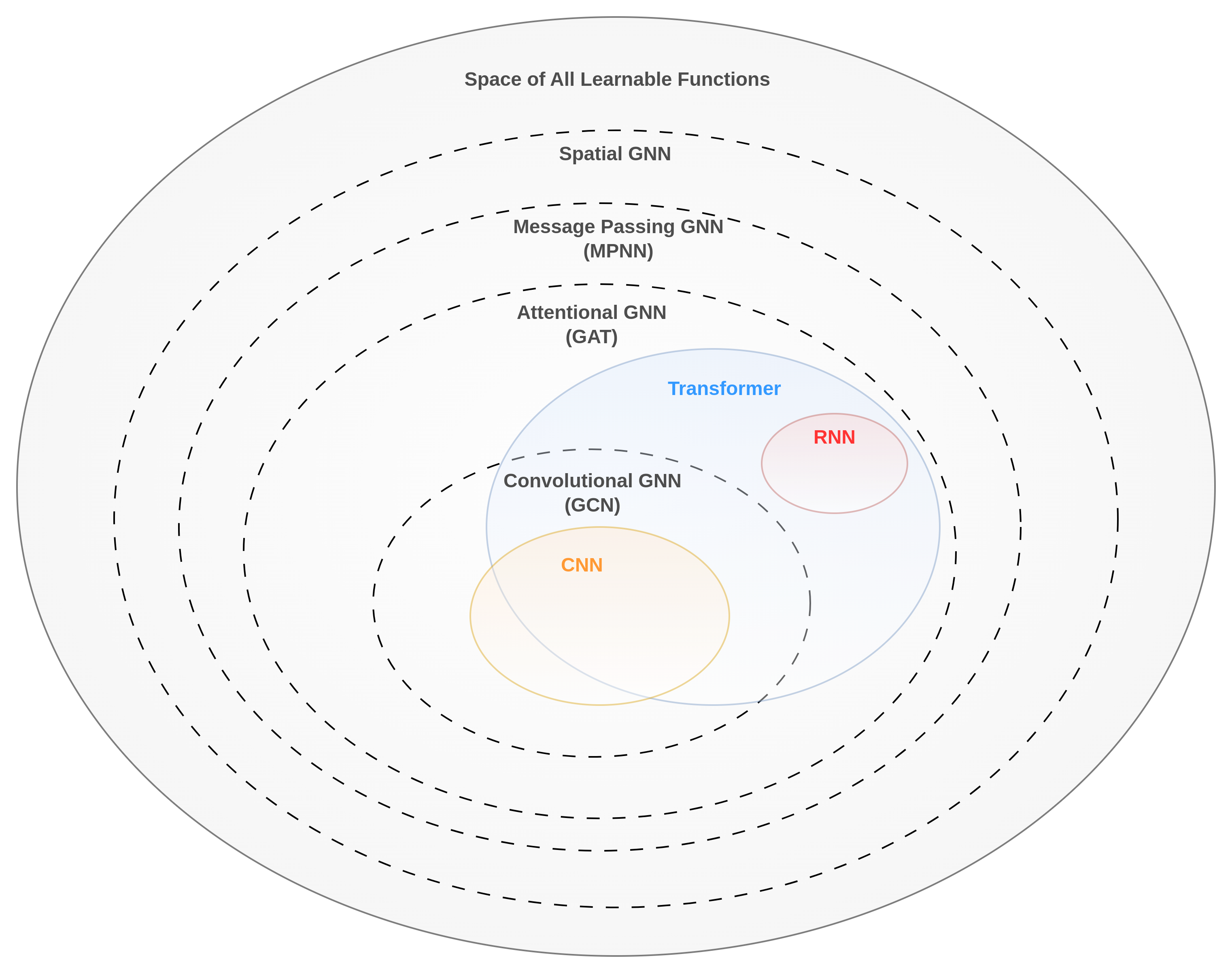
RNNは[2]よりGPTなどのテキスト生成モデルで扱われるようなCausal Maskingで学習されたTransformerと等価します.TransformerはCNNで学習可能な関数の殆どを学習できますが、CNNで学習されるフィルター係数に和が1となる非負の係数の制約がないためTransformerとは異なるメッセージ集計時に凸包外のベクトルを算出する関数を学習できます.
まとめ
- CNNやTransformerなどのモダンネットワークはSpatial GNNのMPNNの特殊ケースと考えることができる.
- GNNの枠組みを考えることで、モダンネットワークなどの関数空間を比較することが容易にできる.
- 関数空間が大きい方が、より高い精度を達成する関数が見つかる可能性があるが探索コストも上がる.よって一つの枠組みが実用上他より優れているとは言えず、タスク、データ量や計算リソースなどに依存してくる.
- 近年Transformerが幅広く使われているが、計算力が上がればより関数空間が広いMPNNなどの枠組みが主流になる可能性も見えてくる.
参考文献:
[1]M. M. Bronstein, J. Bruna, T. Cohen, and P. Veličković, “Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges,” arXiv:2104.13478 [cs, stat], May 2021, Accessed: Sep. 19, 2021. [Online]. Available: http://arxiv.org/abs/2104.13478
[2]A. Katharopoulos, A. Vyas, N. Pappas, and F. Fleuret, “Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention,” arXiv:2006.16236 [cs, stat], Aug. 2020, Accessed: May 27, 2021. [Online]. Available: http://arxiv.org/abs/2006.16236
[3]J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural Message Passing for Quantum Chemistry.” arXiv, Jun. 12, 2017. Accessed: Jun. 04, 2022. [Online]. Available: http://arxiv.org/abs/1704.01212
[4]I. Schlag, K. Irie, and J. Schmidhuber, “Linear Transformers Are Secretly Fast Weight Memory Systems,” arXiv:2102.11174 [cs], Feb. 2021, Accessed: Jun. 04, 2021. [Online]. Available: http://arxiv.org/abs/2102.11174

コメント