これまで (~2023年) の同変性に関して代表的な論文から、幾つか選定してキーポイントをリスト化してみました.ここで、紹介する論文は以下の5本となります.
- E(n) Equivariant Graph Neural Networks
- Equivariant message passing for the prediction of tensorial properties and molecular spectra
- E(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials
- Generalizing Convolutional Neural Networks for Equivariance to Lie Groups on Arbitrary Continuous Data
- B-Spline CNNs on Lie Groups
流れが少しでも把握できるように、一番新しいものから並べて複数の関連性がある論文を紹介しています.ここでは、幾つかの要点のみを記載しています.論文を読む前にこれらを把握することで、皆さんが内容を素早く吸収できることを目的としています.
E(n) Equivariant Graph Neural Networks
著者:Victor Garcia Satorras, Emiel Hoogeboom, Max Welling
発行日:2021年02月19日
最終更新日:2022年02月16日
URL: http://arxiv.org/pdf/2102.09844v3
カテゴリ:Machine Learning, Machine Learning
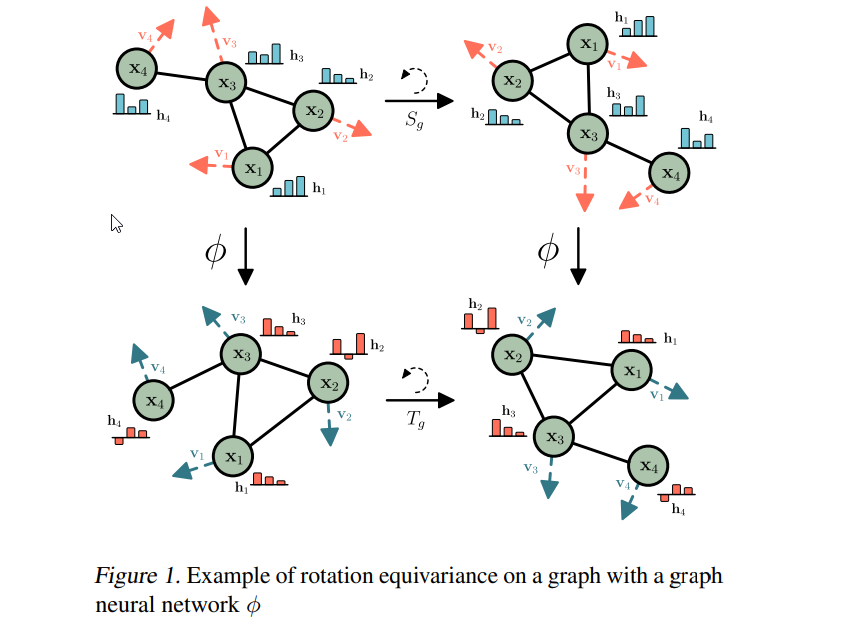

要点:
- Equivariant graph neural networksは、分子やその性質を分析するための新しいツールとして、自然科学や医学からますます注目されています.
- 多くの問題は3Dの平行移と回転の対称性を示す.例えば、点群、3D分子構造、N体粒子シミュレーションなどがある. これらの対称性に対応する群は、Euclidean groupであり、反射を含める場合はE(3)である.
- E(3)またはSE(3)同変性を達成するための様々な形式や方法が提案されている.
- 高次元表現の研究において、多くの作品が革新を達成している. ただし、これらの高次元表現の変換には、計算コストが高い係数や近似が必要となる場合がある.
- この研究では、計算効率が高く、実装が容易であり、幅広いタスクにおいて現在の最先端を大幅に改善する新しいE(n) equivariant deep architecture for graphsを提案しました.
- このモデルは、回転、平行移動、反射、置換に対して等変なグラフニューラルネットワークを学習することができます.
- 既存の手法とは異なり、中間層で高次元表現を計算する必要がなく、競合力のあるまたはより良い性能を実現しています.
- このモデルは、より高次元空間に簡単にスケーリングできます.
- このモデルは、以前の手法と比較して、球面調和関数を必要としないため、よりシンプルである.
- この手法の効果を、動的システムモデリング、グラフオートエンコーダーにおける表現学習、分子特性の予測において実証しています.
- これらの特性により、薬剤探索、タンパク質の折りたたみ、新しい材料の設計などのトピックに直接的な影響を与えるのに最適であり、3Dコンピュータビジョンの応用にも適していると考えられています.
Equivariant message passing for the prediction of tensorial properties and molecular spectra
著者:Kristof T. Schütt, Oliver T. Unke, Michael Gastegger
発行日:2021年02月05日
最終更新日:2021年06月07日
URL: http://arxiv.org/pdf/2102.03150v4
カテゴリ:Machine Learning, Chemical Physics
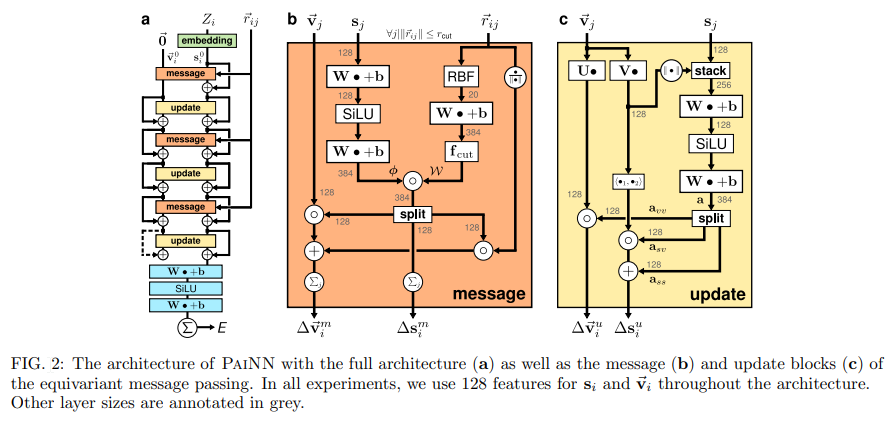
要点:
- メッセージパッシングニューラルネットワークは、グラフ上での学習の選択手段となっており、特に化学的特性の予測や分子動力学研究の加速に使用されています.
- これらは大規模なトレーニングデータセットに簡単にスケーリングできますが、従来のアプローチはカーネル法よりもデータ効率が低いことが証明されています.
- 同変MPNNの設計の一般的なガイドラインを提供し、計算効率性や方向情報の伝播能力などの観点から、同変表現の利点について説明した.
- これに基づいて、Polarizable Atom Interaction Neural Network ( PaiNN ) を提案し、スカラーおよびテンソリアル分子特性の迅速かつ正確な予測を実現した.
- PaiNNによって得られた同値原子単位の表現を活用して、テンソリアルプロパティの予測に利用します.
- PaiNNは、
- 回転不変性のみを持つモデルよりも高い精度を出すことができる.
- 同変メッセージパッシングにより、方向性メッセージパッシングと比較して、モデルサイズと推論時間を大幅に削減しながら、精度を維持できる.
- 小さなサンプルサイズでも、ニューラルネットワークよりもデータ効率が高いとされるカーネル法と同等の精度を出すことができる.
- ンソル特性の予測にも適用することができる.
- PaiNNによって、赤外線スペクトルとラマンスペクトルのシミュレーションが4-5桁高速化され、1つの場合では25年かかるところを1時間に短縮できる.
- PaiNNはPyTorchとSchNetPackを使用して実装されている.
- 将来的には、PaiNNの同変表現やテンソリアル特性の予測能力を、3Dジオメトリの生成モデルや波動関数の予測に活用することができる可能性がある.
その他の情報
- MPNNは、
- グラフ構造を持つ分子の表現に適している.
- 分子の性質の予測において、
- 高い精度を持つ.
- 計算時間を短縮することができる.
- 既存の手法よりも高速である.
- データ効率が高い.
- 様々な応用が可能である.
- 3D形状認識やグラフ埋め込みなどの分野でも利用されている.
- 機械学習は、原子レベルのシミュレーションにおいて、ポテンシャルの予測や高速化に役立つ可能性がある.
E(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials
著者:Simon Batzner, Albert Musaelian, Lixin Sun, Mario Geiger, Jonathan P. Mailoa, Mordechai Kornbluth, Nicola Molinari, Tess E. Smidt, Boris Kozinsky
発行日:2021年01月08日
最終更新日:2021年12月16日
URL: http://arxiv.org/pdf/2101.03164v3
カテゴリ:Computational Physics, Materials Science, Machine Learning
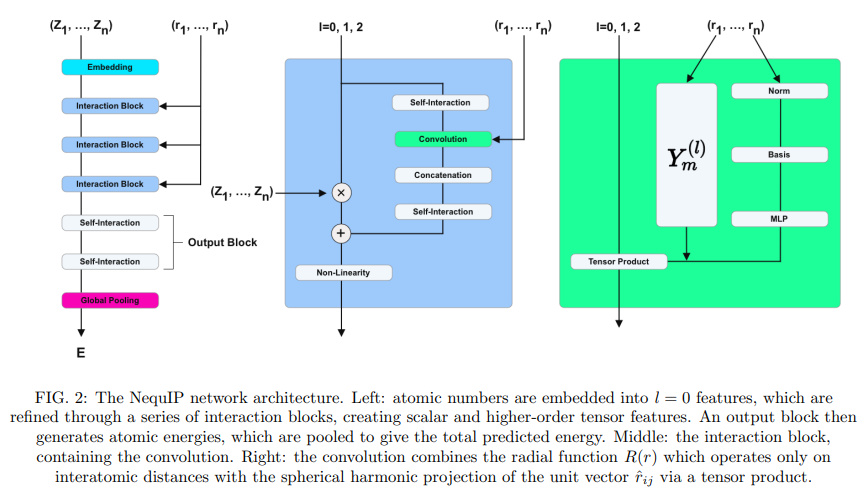
要点:
- Neural Equivariant Interatomic Potentials(NequIP)は、分子動力学シミュレーションのためのab-initio計算から相互原子ポテンシャルを学習するためのE(3)-equivariantニューラルネットワークアプローチである.
- NequIPは、
- 幾何学的テンソルの相互作用にE(3)-equivariant畳み込みを使用し、より情報豊富で忠実な原子環境の表現を実現している.
- 難解で多様な分子や材料のセットに対して最先端の精度を実現し、驚異的なデータ効率を発揮している.
- データ効率性に関して、
- 既存のモデルよりも3桁少ないトレーニングデータで最高の性能を発揮し、深層ニューラルネットワークが大量のトレーニングセットを必要とするという広く信じられている考えに挑戦している.
- 1000個以下、あるいは100個の参照データからでも正確な原子間ポテンシャルを構築することができる、データ効率に優れた手法である.
- 少ない数の第一原理計算から高精度な原子間ポテンシャルを構築することができる. 他の方法が桁違いに多くの参照ab-initio計算を必要とするのに対し、100個未満、さらには100個程度の参照ab-initio計算で高い予測精度を実現するニューラルネットワークである.
- 小規模な分子データセットでは、他のニューラルネットワークだけでなく、カーネルベースの手法にも競争力を持っており、通常、トレーニングと予測のスケーリングにかなりの追加コストがかかるカーネルベースの手法よりも予測精度が高い.
- 高いデータ効率により、高次量子化学レベルの理論を参照として正確なポテンシャルを構築することが可能になっている.
- 既存の機械学習を用いた原子間ポテンシャルと比較して高い精度を示す.
- 小分子や水、アモルファス固体、固体/気体界面での反応、リチウム超イオン伝導体など、様々な系に対して適用可能である.
- NequIPを使用することで、高次の量子化学レベルを基準としてポテンシャルを計算することができる.長時間スケールで高精度な分子動力学シミュレーションが可能になる.
その他の情報
- 紹介された新たな手法の背景、
- 分子動力学シミュレーション(MD)は、エネルギー貯蔵、触媒、生物学的プロセスなど、多様な分野で計算的発見に不可欠なツールである.
- ニュートンの運動方程式を積分するために必要な原子力は、原子密度決定理論(DFT)などの量子力学的計算から高い信頼性で得ることができるが、第一原理法の計算の不利なスケーリングにより、現実的にはシミュレーションは短時間スケールと小規模な原子数に限定される.これにより、現在アクセス可能な時間と長さのスケールを超えた多くの興味深い物理現象の研究が制限される.
- 原子ポテンシャルエネルギーのための古典的モデルは、その単純な機能形式のために、第一原理法よりも桁違いに高速に評価できるため、長時間スケールで多数の原子の研究が可能になる.しかし、数学的に限定されているため、精度が制限される.
- 古典的な原子間ポテンシャル、または力場は、時間スケールに応じてシステムのダイナミクスを予測するために限界がある.
- Machine Learning Interatomic Potential (ML-IP) に基づく柔軟な原子間ポテンシャルエネルギーモデルの構築、特に Neural Network Interatomic Potential (NN-IP) は、このジレンマを乗り越える方法を提供することができる.
- これにより、ab-initio参照計算から高精度のポテンシャルを学習しながら、計算効率を維持することができる.
- NN-IPの制限因子の1つは、通常、数千または数百万の参照計算を含む大規模なトレーニングセットの収集が必要であることである.この問題を解決するため、NequIPという手法が提案された.
Generalizing Convolutional Neural Networks for Equivariance to Lie Groups on Arbitrary Continuous Data
著者:Marc Finzi, Samuel Stanton, Pavel Izmailov, Andrew Gordon Wilson
発行日:2020年02月25日
最終更新日:2020年09月24日
URL: http://arxiv.org/pdf/2002.12880v3
カテゴリ:Machine Learning, Machine Learning
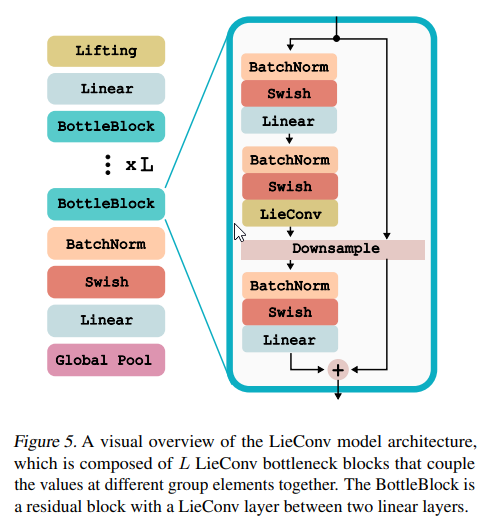
要点:
- 指数写像が全射である任意の指定されたリー群の変換に同変性を持つ畳み込み層を構築する一般的な方法を提案しています.
- LieConvを提案:畳み込み演算をLie群上で実行するための手法.新しい群で同変性を組み込むには、指数関数と対数関数を実装するだけでよく、迅速なプロトタイピングが可能になります. 殆どの場合、Lie群は無限小生成子(Lie代数)のベクトル空間を用いてパラメータ化できる.
- LieConvは、
- Lie群からの変換に同変な畳み込み層であり、非等質空間や任意の空間データに適用できます.
- 画像分類ベンチマークデータセットrotMNISTと回帰ベンチマークデータセットQM9で評価され、QM9のいくつかのタスクで最新の手法を上回り、競合力のある結果を実現しています.
- 物理系のハミルトニアンモデリングにLieConvを適用すると、等変性は物理量(エネルギー、角運動量など)の保存に対応します.
- 動的システムのモデリングにおいて最新の手法を上回ります.
- 方法の簡単さと汎用性を示すために、同じモデルアーキテクチャを画像、ボールアンドスティック分子データ、およびハミルトニアン力学系に適用しています.このモデルの同変性は特に影響力があり、線形運動量と角運動量の正確な保存をもたらします.
その他の情報
- LieConvによるコードは、https://github.com/mfinzi/LieConvで入手できます.
B-Spline CNNs on Lie Groups
著者:Erik J Bekkers
発行日:2019年09月26日
最終更新日:2021年03月22日
URL: http://arxiv.org/pdf/1909.12057v4
カテゴリ:Machine Learning, Machine Learning
要点:
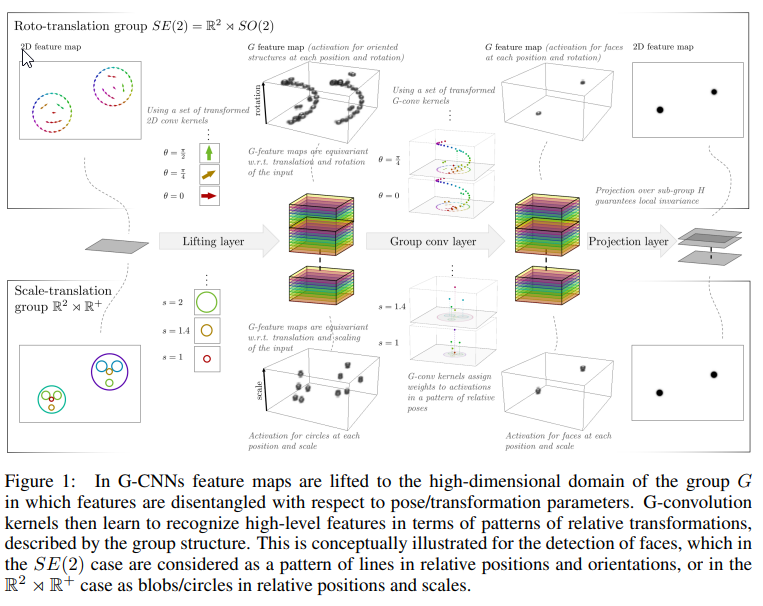
- グループ畳み込みニューラルネットワーク(G-CNN)は、古典的なCNNを群の幾何学的構造で装備することによって改善することができます.
- G-CNNの成功の中心は、特徴マップを高次元の分離された表現にリフトアップすることであり、そこではデータ特性が効果的に学習され、幾何学的なデータ拡張が不要になり、幾何学的変換に対する予測可能な振る舞い(同変性)が群理論によって保証されます.
- G-CNNの文献は、離散的なG-CNN、定常的な連続G-CNN、およびステアリング可能な連続G-CNNに分けられる.
- 現在のG-CNNの実装は、グリッドをそのままにする離散的な群または回転などの連続的なコンパクトな群に限定されています.
- 本論文では、これらの制限を解除し、任意のリー群に対するG-CNNの設計と実装のためのモジュラーなフレームワークを提案しています.
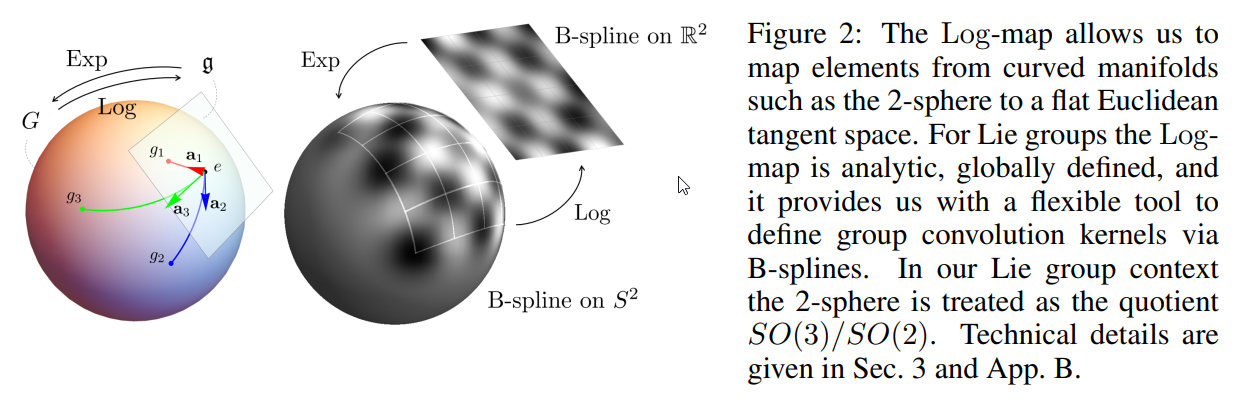
- 我々のアプローチでは、リー群の微分構造を用いて、リー代数上に定義された一般的なBスプラインの基底で畳み込みカーネルを拡張します.
- Bスプラインに関して、
- Bスプラインは、局所的なサポートを持つ分段多項式であり、古典的には平坦なEuclidean空間 \( \small \mathbb{R}^d \) 上で定義されている.
- 本論文では、BスプラインをLie群に一般化し、Lie群の微分構造を使用して定義している.
- B-スプラインをリー群に適用し、リー群の微分構造を用いて定義を行うことで、B-スプラインは対数写像によって得られるリー代数の(平坦な)ベクトル空間上で本質的に定義されるという柔軟な枠組みが得られる.これにより、従来のフーリエ型基底展開法では実現できない、局所化、アトラス、変形可能な畳み込みを、それぞれ局所化された、疎で非一様なB-スプラインを用いてG-CNNsで構築することができる.
- Bスプラインは、リー代数上に定義された汎用的な基盤であり、これにより、局所的、atrours (dilated)、および変形可能な畳み込みをG-CNNで実現できる柔軟なフレームワークが可能になる.
- Bスプライン基底関数は、リー群上の滑らかなピクセルと考えることができ、古典的なCNN設計の馴染みのある概念を使用してG-CNNを設計することを可能にする
- 提案されたアプローチは、Lie群上のBスプラインの定義に依存しており、これを使用してグループ畳み込みカーネルを拡張し、サンプリングしている.
- 本論文では、スケール同変性も組み込まれたG-CNNを検証し、回転移動を超えた同変性を実現するためのG-CNNの最初の直接的な応用です.
- このアプローチの影響と可能性は、回転同変性が重要な組織学的スライドの癌検出と、スケール同変性が重要な顔のランドマークのローカリゼーションの2つのベンチマークデータセットで研究されている.
- atroursおよび局所的なグループ畳み込みの付加価値が詳細に研究されている
- 局所化された、疎で非一様なBスプライン展開によって、G-CNNで局所化された、疎で変形可能な畳み込みが可能な柔軟なフレームワークが実現される
- B-スプライン基底関数は、古典的なフーリエ基底関数では実現できないユニークな特性を持っている
- 2つの異なる群を考慮した2つの異なるアプリケーションで、局所化されたおよび atrours グループ畳み込みの付加価値を実験的に示している
その他の情報
- Worrall&Welling(2019)などでは、スケール不変層を構築するためにスケール空間理論と半群理論を使用しており、スケーリングによる移動バンドリミットをエレガントに処理しています.私たちの研究はいくつかの点で異なりますが(例えば、学習されていないリフティング層、atroursカーネルを介した離散グループ畳み込み、半群理論)、深いスケール空間ネットワークの最初の2つの層は、私たちのB-スプラインを、(Worrall&Welling、2019)の半群作用によって変換されたディラックデルタの重ね合わせとして扱うことによって、私たちのリフティング層に関連しています.



コメント