はじめに
概略として幾つかの数学用語を用いて簡潔に紹介いたします.その後にそれらの用語について詳しく説明していこうと思いますので、ここではまず全体像を掴んでいただけるように書いていきます.
ニューラルネットでの同変性 ( equivariance ) は、データ構造の対称性を活用することでデータに適切な構造を保持する写像のみに学習可能な関数空間を制約する帰納バイアスです.厳密には、深層学習の演算子を群の作用上の準同型写像または繋経絡作用素(intertwiner) という関数の集合に絞って学習が行われるようになります.新たな概念に思えてしまいますが、同変性はCNNやTransformerなどにも組み込まれているモダンネットワークの設計に欠かせない概念であり、表現学習が成功している大きな理由の一つです.一般的に2次元画像データより3次元空間データなどの自由度が高いデータで高い効果が発揮され、有名な例としてはAlphaFold2です.
同変性を組み込むことで、中間層の表現が普段使われているユークリッド空間上のベクトル場に限らず、より一般的な空間上でのベクトル場であるファイバー束を扱うことが可能になります.例えば、球面上のパノラマ画像をネットワークで処理するさいに、球という構造を群の剰余類としてファイバー束の底空間(base space)に組み込むことで、中間層でも球という構造を保ったまま幾何学的に正しい学習が行えるようになりました.これは、同変ニューラルネットワークによる大きな貢献の一つだと思います.
研究は2016の[1]を起点に進んでおり、大きく見て以下の2種類の項目に分かれます.
- 等質空間上 ( homogeneous space ) の深層学習
- 群上の畳み込み、または、群の正則表現による深層学習 ( group convolution – regular representation )
- 操作可能な畳み込み、または、群の誘導表現による深層学習 ( Steerable Convolution – induced representation )
- 多様体上 ( manifold ) の深層学習
1と2は、データ構造によって分けられています.1は2次元画像や球面上のパノラマ画像など規則性が高いものの幾何学的構造を事前知識としてモデルに組み込みます.これらの構造は対称性を効率良く活用できるために、多くの重みが共有または削除 (ゼロになる) され、スパースで汎化性能が高いネットワークが作成されます.これは、CNNの畳み込み処理を一つの巡回行列 ( circulant matrix ) の掛け算として表した時に、殆どの重みはゼロで多くの重みが共有されるイメージと同様です.CNNは並進変換の対称性( ※他にも局所性 )を活用することで、全結合層と比較してかなりスパースになり、より画像データに対して汎化性能が高いネットワークになりました.2の多様体上の深層学習は、1での等質空間という制限に縛られず、任意の多様体を底空間に持つ枠束 (frame bundle) を用いた表現へと拡張しています.
冒頭で述べた通り、同変性はあるデータ構造を前提としたバイアスとなるので、Bias vs. Variance Trade-offが生じます.適切なバイアスを組み込めば、少量のデータでも汎化性能が高いモデルの作成が見込めますが、誤ったバイアスを用いると精度は悪化します.
Convolution Neural Network (CNN)から説明する同変性
CNNは並進変換に対して同変
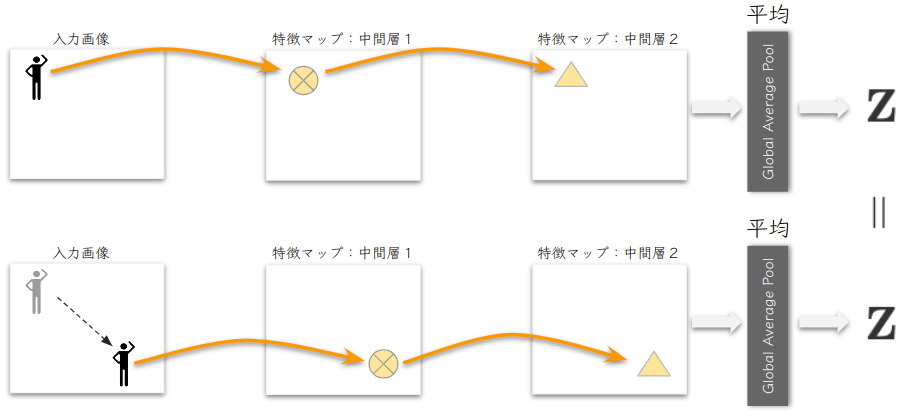
同変 (equivariance) であることは、中間層の情報が、入力と同じ用に動くことです.これは、「共変」( covariance )という用語が一般的に使われますが、群の作用に対して同じ用に動くということで弁別されています.以下の図のようにCNNでは、入力画像に現れる対象に並進変換を与えても中間層で対象を表現する情報 ( 例えばスカラー、ベクトルやテンソルなど ) が同じように動き、情報そのものは変わりません ( \( \small \bigotimes \) は \( \small \bigotimes \) のまま、△も△のまま).これが並進変換((\( \small \mathbb{Z},+ \))群の作用)にての同変性です.ネットワークが同変であれば、Global Average Pool で平均化したあとのベクトルによる表現 \( \small \mathbf{Z} \) が入力画像の並進変換に対して不変となり、分類タスクで位置に依存しない正しい判定ができるモデルになります.よって、一箇所のみで対象を学習しても、他の位置に現れた対象を正しく認識できる汎化性能が高いモデルになります.
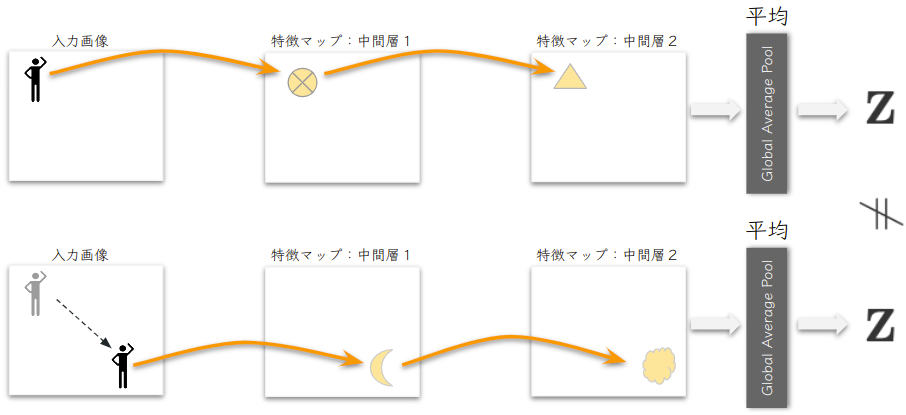
しかし逆に同変性が成立しない場合は対象の位置を変えると以下ののようにベクトル \( \small \mathbf{Z} \) が不変になりません.そうなると、対象の位置によって誤認識しやすいモデルになります.
CNNは回転変換に対して同変ではない
問題は回転変換 (\( \small SO(2) \)群の作用に) に対してCNNは同変ではありません.よって、特徴マップの情報は回転させることで変化してしまう可能性があり、角度が変わっただけで正しく認識されなくなる恐れがあります.この問題に対して普段使われる対処法は画像認識モデルの作成時に回転変換を用いた水増しを行うことです.
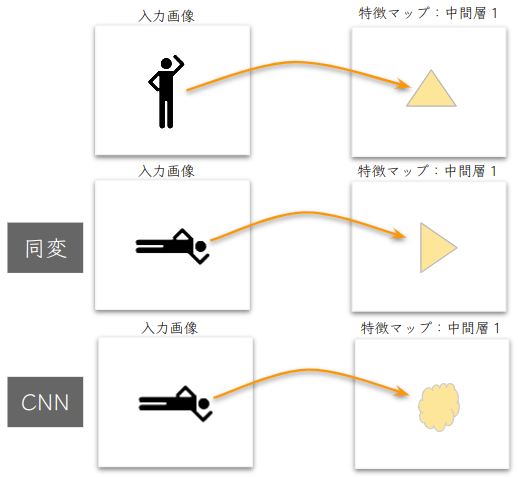
水増しを使うのではなく、CNNが並進変換に対しての同変性を内在的に備えているように、ネットワークに回転変換に対しての同変性も組み込もうというのが [1] の研究です.この話を進めるには、まずCNNの演算を群の作用に書き換え抽象化することで、自然に演算子を回転変換にも同変なものに拡張していきます.
CNNの演算子を群の作用に書き換える
CNNで行われる演算は、厳密には畳み込みではなくて、相互相関を行っています.演算子を数式で表すと以下となります. $$ \small f_{out}(x) = (k \star f_{in})(x) := \int_{\mathbb{R}^2} k(y)f_{in}(y+x) dy \tag{1}$$ 2次元画像の位置: \( \small x,y \in \mathbb{R}^2 \)
入力特徴マップ: \( \small f_{in}: \mathbb{R}^2 \rightarrow \mathbb{R}^{C_{in}} \)
出力特徴マップ: \( \small f_{out}: \mathbb{R}^2 \rightarrow \mathbb{R}^{C_{out}} \)
フィルター: \( \small k:\mathbb{R}^2 \rightarrow \mathbb{R}^{C_{out}} \times \mathbb{R}^{C_{in}} \)
実際にコンピューター上で扱われる演算は連続型の\( \small \mathbb{R}^2 \)上ではなく、離散型の\( \small \mathbb{Z}^2 \)上ですが後で離散型に置き換えることもできるので、利便性からも連続型で話しを進めていきます.(1) は入力特徴マップに並進変換を与えてカーネル \( \small k \) と内積しているという見方ができます.この並進変換を関数 \( \small f \in \mathcal{X}=\{g:\mathbb{R}^2 \rightarrow \mathbb{R}^C\} \) に作用する群 \( \small G = (\mathbb{R}^2,+) \) の作用 \( \small \mathbb{T}_x: \mathcal{X}\times G \rightarrow \mathcal{X} \) を以下の用に定義して、それに(1)を書き換える作業を行っていきます. $$ \small
\begin{equation}
\begin{split}
\mathbb{T}_x(f)(y) := f(y-x)\ \\
\Rightarrow \mathbb{T}_{x^{-1}}(f)(y) =f(y+x)
\end{split}
\end{equation}
\tag{2}
$$ ※ (2) の定義が群の作用の公理を満たすこと確認してみて下さい.
(1)の\( \small f_{in}(y+x) \)を(2)に置き換えて内積で表すと以下のようになります. $$ \small
\begin{equation}
\begin{split}
(k \star f_{in})(x) &= \int_{\mathbb{R}^2} k(y)\mathbb{T}^{in}_{x^{-1}}(f_{in}) (y)dy\ \\ &= \langle k, \mathbb{T}_{x^{-1}}(f_{in}) \rangle_{\mathbb{R}^2}
\end{split}
\end{equation}
\tag{3}
$$ これで、CNNの演算子を群の作用の形式に書き換えることができました.次はこれが、任意の並進変換群の作用 \( \small \mathbb{T}_t \) を入力特徴マップに与えることで並進変換群の作用に対して同変であることを確認します. $$ \small
\begin{equation}
\begin{split}
(k \star \mathbb{T}^{in}_t(f_{in}))(x) & = \int_{\mathbb{R}^2} k(y)\mathbb{T}^{in}_{x^{-1}}\mathbb{T}^{in}_t(f_{in})(y)dy \ \\
& = \int_{\mathbb{R}^2} k(y)f_{in}(y+x-t)dy \ \\
& = \int_{\mathbb{R}^2} k(y)f_{in}((x-t)+y)dy \ \\
& = f_{out}(x-t)=\mathbb{T}^{out}_t(f_{out})(x) \ \\ \\ \\
\Rightarrow (k \star \mathbb{T}^{in}_{t}(f_{in}))(x) &= \mathbb{T}^{out}_{t}(f_{out})(x),\forall t \in (\mathbb{R}^2,+)
\end{split}
\end{equation}
\tag{4}
$$ 入力特徴マップへ与えた群の作用が出力特徴マップにも同じように与えられているのが分かります.これがCNNの同変性です.
Group Convolution の定義
抽象化して他の任意の群の作用に同変である Group Convolution を定義する
CNNを並進変換群の作用に同変な特殊ケースと捉え、任意の群の作用に拡張したのが group convolution (※ PytorchライブラリやResNextなどので定義される group convolution とは全く異なるものなので注意 )です.まずは、(2)を任意の群\( \small G \)へ拡張して群の作用を以下で定義します. $$ \small \rho^{in}_g (f)(s) : = f(g^{-1}s) \ \ \forall g,s \in G \tag{5}$$ ここで、(5)の \( \small \rho^{in}_g \) が線形であることが以下の2つの公理を満たしていることで確認できます.任意の\( \small f,h \in \mathcal{X} \)と\( \small a \in \mathbb{R} \) にたいして、 $$ \small
\begin{equation}
\begin{split}
\ \rho_g^{in} (f+h)(s) &= (f+h)(g^{-1}s) =f(g^{-1}s)+h(g^{-1}s)\ \\
&=\rho_g^{in} (f)(s)+\rho_g^{in} (h)(s)
\end{split}
\end{equation}
\tag{加法的}
$$ $$ \small
\begin{equation}
\begin{split}
\ \rho_{g}^{in}(af)(s) &= (af)(g^{-1}s) = a (f(g^{-1}s)) \ \\
&= a \rho_{g}^{in}(f)(s)
\end{split}
\end{equation}
\tag{斉次的}
$$ ベクトル空間に作用する群の線形作用を群の表現と呼びます.群の表現は幾つかのタイプがあり、(5)のようにベクトルの基底を置換するような群の表現は正則表現 ( regular representation ) と呼ばれます ( 詳しくは[3]を参照 ) .そして、以下が group convolution の定義となります. $$ \small
\begin{equation}
\begin{split}
f_{out}(g) &= \langle k, \rho^{in}_{g^{-1}}(f_{in}) \rangle_{G} \ \\
&= \int_{s \in G} k(s)\rho^{in}_{g^{-1}}(f_{in})(s)d\mu(s)
\end{split}
\end{equation}
\tag{6}
$$ 内積は今まで2次元の次数空間 \( \small \mathbb{R}^2 \) で行われましたが、それをより一般化して群\( \small G \)上で内積を行います.群上で積分を定義するには適切な測度が必要となります.そこで、群の作用に対して不変であるハール測度 \( \small d \mu \) を用いて積分を定義することで、局所コンパクトな位相を持つ群上で積分が成立します.つまり、group convolution の制約は、局所コンパクトな群に限られることになりますが、これはかなり弱い制約なので適用範囲はかなり広いです.これから扱う連続群は全て多様体構造をもつので、それに該当することになります.
(6)の積分が群の作用に対して不変であることと、作用の定義(5)を用いれば以下の性質が導けます. $$ \small \langle k, \rho^{in}_{g^{-1}}(f_{in}) \rangle_{G} =\langle \rho^{in}_{g}(k), f_{in} \rangle_{G} \tag{7}$$ これを使うと、以下のようにgroup convolution が任意の\( \small h \in G \)の群の作用に対して同変であることが容易に確認できます. $$ \small
\begin{equation}
\begin{split}
\langle \rho^{in}_{g}(k), \rho^{in}_{h}f_{in} \rangle_{G} &=\langle \rho^{in}_{h^{-1}}\rho^{in}_{g}(k), f_{in} \rangle_{G}\ \\
&=\langle \rho^{in}_{h^{-1}g}(k), f_{in} \rangle_{G}\ \\ &= f_{out}(h^{-1}g)=\rho^{out}_h(f_{out})(g)
\end{split}
\end{equation}
\tag{8}
$$
畳み込みと同変性
次はより一般的な \( \small G \) 同変である写像 \( \small \Phi:\mathcal{X}_{in} \rightarrow \mathcal{X}_{out} \) を考えたとき、\( \small \Phi \) は群の表現と可換することになります. $$ \small \forall g \in G, \ \Phi \circ \rho_{g}^{in} = \rho_g^{out} \circ \Phi$$
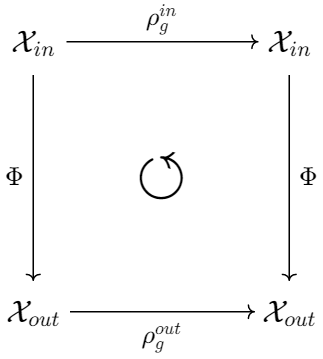
ニューラルネットワークで\( \small \Phi \) は任意のフィードフォワード処理となります.group convolution の定義 (6) が同変であることが確認されましたが、他にどのよう演算子 \( \small \Phi \) が同変性を満たすのでしょうか?\( \small \Phi \) を有界線形作用素に絞った時、[2] ではそのような \( \small \Phi \) が同変であるには、\( \small \Phi \) が必然的に相互相関関数 (または、畳み込み) であることが示されています.つまり、GPU上で行列掛け算を行う深層学習のフィードフォワード処理では、処理の形式を ( 6 ) のように畳み込みで表せることが同変性を組み込める必要十分条件となります.ここで、気を付けなければいけないのは「畳み込み」と聞くとCNNをイメージしてしまいますが、Transformerなども畳み込み形式で表せるので同じく同変性を組み込むことができます.
Group Convolution の例
簡単な例として[1]で扱われている \( \small p4m \) 群がありますが、ここでは、更にシンプルな \( \small p4 \) 群を例として演算処理を見ていこうと思います.その前に2次元画像の Group Convolution の一般形式を紹介してから \( \small p4 \) 群を特別な例として話を進めていきます.CNNはGroup Convolution の群が \( \small (\mathbb{R}^2,+) \)である特殊ケースですが、回転群 \( \small SO(2) \) への同変性も組み込むには回転も含んだ群に置き換える必要があります.そこで、これらの群の半直積から構成される2次元特殊ユークリッド群 \( \small SE(2)=(\mathbb{R}^2,+) \rtimes SO(2) = \{ tr |t \in (\mathbb{R}^2,+), r \in SO(2) \} \) を使います.更に鏡映への同変性を追加するには2次元ユークリッド群 \( \small E(2)=(\mathbb{R}^2,+) \rtimes O(2) \) を使います.\( \small SE(2) \) は \( \small E(2) \) の 部分群であり、より大きい群を用いることで、より強い対称性を組み込むことができます.これは、より強い帰納バイアスでもあり、不適切なものを用いれば精度の悪化へと繋がります.例えば、鏡映の同変性を分類タスクに用いた場合、鏡映に対しての不変性が促されるので上下、左右の違いに基づく識別が不可能になります.これでは左か右車線用の車を運転座席の位置から推定したいタスクなどでは、識別不能になってしまいます.
これから細かく見ていく\( \small p4 \) や \( \small p4m \) 群は離散型で比較的小さな群ですが、\( \small SE(2) \) や \( \small E(2) \) の元は連続的であるので大きく、大きさの順番は小さい方から \( \small p4 \subset p4m \subset SE(2) \subset E(2) \) となります.\( \small p4 \) は離散型並進変換群 \( \small (\mathbb{Z}^2,+) \) と0,90,180,270度の4つの回転からなる群 \( \small C_4 \) との半直積となるため、\( \small SE(2) \) の粗い離散型バージョンというイメージです.\( \small p4m \) は \( \small p4 \) に鏡映を追加したものです.
\( \small p4 \) Group Covolution 第1層 (Lifting layer)
最初の層は、入力画像 \( \small f_0:\mathbb{Z}^2 \rightarrow \mathbb{R}^{C_0} \) を特徴マップ\( \small f_1:G \rightarrow \mathbb{R}^{C_0} \) へ写します.ここで注意するのは、group convolution の定義 (6) に現れる入力と出力の特徴マップが画像上の関数 (\( \small \mathbb{Z}^2 \) 上の関数) ではなく、群 \( \small G \) 上の関数であることです.入力画像は \( \small G=p4 \) の部分群である\( \small \mathbb{Z}^2 \) 上の関数であるため、\( \small G \) 上の関数にリフトしてあげるという意味で特別に lifting layer という名が付いています.任意の\( \small g=tr \in p4, \ t\in \mathbb{Z}^2, \ r \in C_4 \) に対して以下が第1層の演算となります. $$ \small
\begin{equation}
\begin{split}
f_{1}(g)
&=\displaystyle\sum_{x \in \mathbb{Z}^2}k(r^{-1}x)f_{0}(x+t) \ \\
&= f_{1}(tr)
\end{split}
\end{equation}
$$ これは、単純に各フィルターを回転させて畳み込みをすることと同じになります.
\( \small p4 \) Group Covolution 第2層以降
第2層以降の特徴マップは全て\( \small G \) 上の関数となり、\( \small G=p4 \) の部分群 \( \small H = C_4 \)とした時に以下の演算で行われます. $$ \small
\begin{equation}
\begin{split}
f_{out}(g) & = \displaystyle\sum_{s \in G}\rho_g(k)(s)f_{in}(s) =\displaystyle\sum_{s \in G}\rho_{tr}(k)(s)f_{in}(s)\ \\
& =\displaystyle\sum_{s \in G}\rho_{t}\rho_{r}(k)(s)f_{in}(s)=\displaystyle\sum_{s \in G}\rho_{r}(k)(s)\rho_{t^{-1}}f_{in}(s)\ \\
& =\displaystyle\sum_{s \in G}k(r^{-1}s)f_{in}(s+t) \ \\
& =\displaystyle\sum_{r’ \in H}\displaystyle\sum_{x \in \mathbb{Z}^2}k(r^{-1}xr’)f_{in}(xr’+t) = f_{out}(tr) \ \ \
\end{split}
\end{equation}
$$
p4 Group Convolution の独立パラメータ
カーネルの行列サイズは以下の表に記載したようにCNNより大きくなりますが、実際の独立パラメータは行列内の一部のみで、第1層のパラメータ数はCNNとおなじです.これは、行列内の多くの重みが共有されているか、疎らになっていることを示唆しています.一般的に同変性を組み込むことで、元のカーネル行列の部分空間が学習される重みとなります.
| カーネル行列のサイズ | 独立フィルター数 | |
|---|---|---|
| 第1層 | \( \small C_{1} \times C_{0} \times \vert H \vert \times k^2 \) | \( \small C_1 \) |
| 第2層以降 | \( \small C_{out} \times C_{in} \times \vert H \vert ^2 \times k^2 \) | \( \small C_{out} \times \vert H \vert \) |
ここでは、\( \small \vert H\vert=|C_4|=4 \)となります.全てのチャンネル数を1としたときの p4群 group convolution の処理の過程を以下の図に表しました.特徴マップは、\( \small p4 \)上の関数となり、1チャンネルで\( \small |C_4|=4 \)枚の2次元画像があるので、図では4枚に展開して表していますが、これらは1チャンネルに値する特徴マップであることが注意点です.
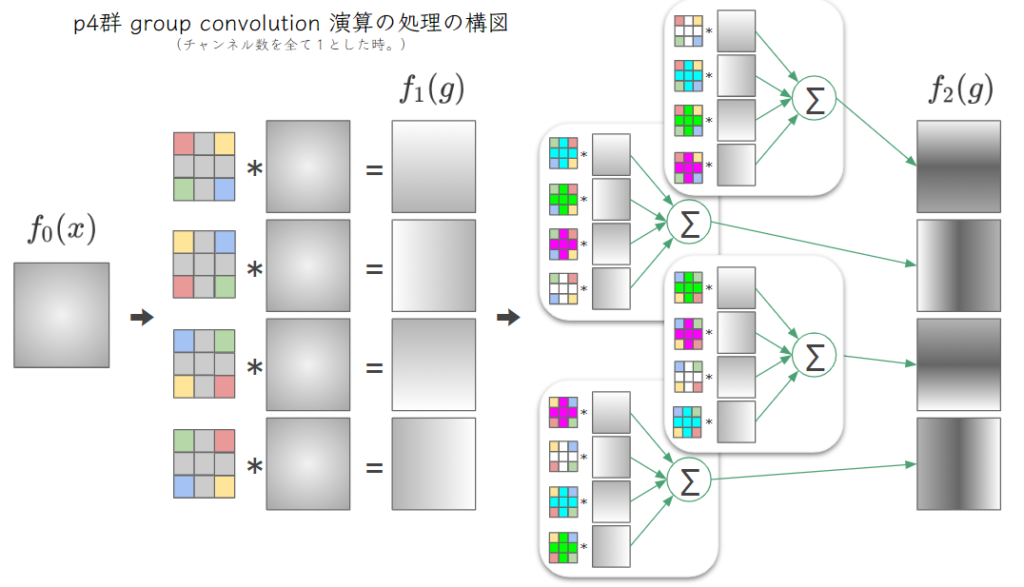
フィルターのかどに色を反時計回りに赤、緑、青、黄の順で付けることで向きを表しています.内部がおなじ色のフィルターは、全く同じフィルターですが向きが異なるだけです.
Global Average Pooling 層
分類タスクなどで行う平均化によるベクトル表現 \( \small \mathbf{z} \) は群上で最後の特徴マップの平均を取ります. $$ \small \mathbf{z} = \frac{1}{|G|}\displaystyle\sum_{g \in G} f_{L}(g) \in \mathbb{R}^{C_L}$$ これが群\( \small G \)の正則表現の作用に対して不変であることを確かめてみてください.
Group Convolutionの問題点
- データタイプや表現がスカラー場に限られる.
- 特徴マップ\( \small f:\mathbb{R}^2 \rightarrow \mathbb{R}^C \) は枚数\( \small C \)のスカラー場として扱われている.
- 群が大きくなると、それに伴って計算量が増えてしまう.
- 群の正則表現に限られるているので、パラメータが膨張しやすい.
- 連続的である無限群には対応できない.
これらの課題を克服するため、群 \( \small G \) そのものの表現を使わず部分群の誘導表現を用いた操作可能な畳み込み ( Steerable group convolution ) を「同変ニューラルネットワークの解説:その 2」で説明していきたいと思います.
まとめ
- CNNは2次元並進変換群 \( \small (\mathbb{R}^2,+) \) に対して同変であるが、回転変換には同変ではない.よって回転変換の水増しが学習時に使われる.
- CNNは 群 \( \small G=(\mathbb{R}^2,+) \) の group convolution の特殊ケースである.
- 回転変換への同変性を追加するのは、group convolution に使う群を回転並進群に置き換えるだけで、回転に同変であれば水増しは必要なくなる.
- 同変性を組み込むことで、元のカーネルの行列に現れる重みが疎らになったり共有されたりする.学習される重みは制約され元のカーネル行列の部分空間内に収まる.
参考文献:
[1]T. S. Cohen and M. Welling, “Group Equivariant Convolutional Networks,” arXiv:1602.07576 [cs, stat], Jun. 2016, Accessed: Mar. 27, 2021. [Online]. Available: http://arxiv.org/abs/1602.07576
[2]T. Cohen, M. Geiger, and M. Weiler, “A General Theory of Equivariant CNNs on Homogeneous Spaces,” arXiv:1811.02017 [cs, stat], Jan. 2020, Accessed: Jun. 27, 2021. [Online]. Available: http://arxiv.org/abs/1811.02017
[3]J.-P. Serre, Linear representations of finite groups, Corr. 5th print. New York: Springer-Verlag, 1996.


